①△BCG≡△DCEであることを証明しなさい。
②BH⊥EDであることを証明しなさい。

 
 
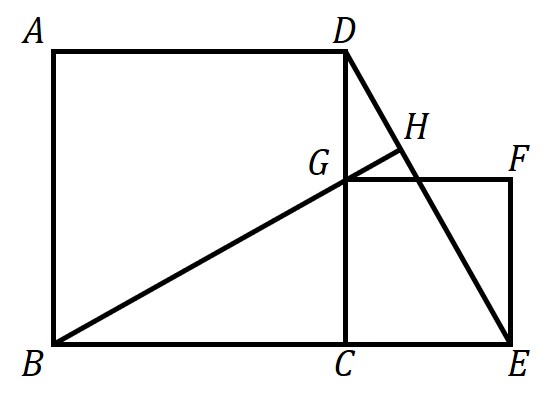
【解説】
①△BCG≡△DCEであることを証明しなさい。

〔方針〕
問題文から、「正方形を組み合わせた図形」が題材になっていることが分かるので、
「直角（90°）や等しい長さの辺がたくさんあって利用できる」と考えます。

〔証明〕

△BCGと△DCEにおいて、
四角形ABCDと四角形GCEFは正方形であるから、
BC＝DC…①
CG＝CE…②
∠BCG＝∠DCE＝90°…③　（←角の大きさが分かっていれば書いておく）　

①、②、③より、
２組の辺とその間の角がそれぞれ等しいので、
△BCG≡△DCE　（証明終わり）
 
 
②BH⊥EDであることを証明しなさい。

〔方針〕
「BH⊥ED」というためには、∠DHG＝90°となっていることを言えばよい。
（垂直に交わるならば、その２つの直線がなす角が90°であるということ）

また、先に①で求めた合同の関係はヒントになっています、
合同の性質から「対応する角の大きさは等しい」こと使いましょう。
これで、△BCGと△DHGが相似であると証明できれば、∠DHG＝90°に言えます。

〔証明〕
△BCGと△DHGにおいて
問題①より、　対応する角の大きさは等しいので、
∠CBG＝∠HDG…④
対頂角は等しいので、∠BGC＝∠DGH…⑤

④、⑤より　２組の角がそれぞれ等しいので、
△BCG∽△DHG
また、相似な図形の対応する角の大きさは等しいので、
∠BCG＝∠DHG＝90°
したがって、BH⊥ED　（証明終わり）

＜まとめ＞

・証明問題では、合同と相似の証明を合わせてすることがある
・「垂直であること」を証明するには、その２つの直線がなす角が90°であることをいう
・角度が等しいことをいうため、相似を証明する