＜ポイント＞
・座標が決まっていない点を考えるときは、「x座標を文字でおく」といい
・問題の条件を読み取り、「どのように設定していけばいいのか」を考える
・点がグラフ上（直線上）にあるのなら、x座標が分かればy座標が分かる
【例題】
関数 y＝－2x＋9 のグラフがx軸, y軸と交わる点を、それぞれA, Bとする。また、直線AB上に点Pをとり、Pからx軸に下した垂線とx軸との交点をQ、y軸に下した垂線とy軸との交点をRとする。
こうしてつくった四角形OQPRが正方形となる、点Pの座標を求めなさい。
【解説】
まず、求めたい点Pのx座標を t とすると、P(t, －2t＋9)となります。
（x,y 以外の文字であれば、どんな文字でおいてもらっても構いません）
関数 y＝－2x＋9 のグラフがx軸, y軸と交わる点を、それぞれA, Bとする。また、直線AB上に点Pをとり、Pからx軸に下した垂線とx軸との交点をQ、y軸に下した垂線とy軸との交点をRとする。
こうしてつくった四角形OQPRが正方形となる、点Pの座標を求めなさい。
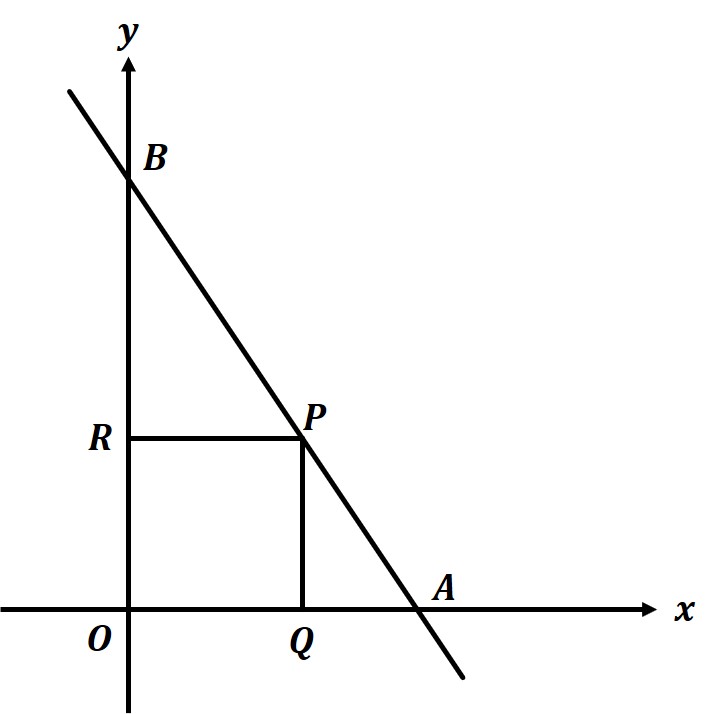
【解説】
まず、求めたい点Pのx座標を t とすると、P(t, －2t＋9)となります。
（x,y 以外の文字であれば、どんな文字でおいてもらっても構いません）
また、「四角形OQPRが正方形となる」という条件を考えると、
「PR＝PQ」となればよいということです。
（↑「どのように設定していけばいいのか」を考えた結果）
PRの長さは「点Pのx座標に等しい」ことから、PR＝t
PQの長さは「点Pのy座標に等しい」ことから、PQ＝－2t＋9
よって、
PR＝PQ
t＝－2t＋9
3t＝9
t＝3 （←点Pのx座標が3ということ）
点Pは直線 y＝－2x＋9 上にあるので、
y＝－2x＋9 に x＝3 を代入して、y＝3
よって、点Pの座標は(3, 3) （答え）
＜補足＞
求める点の座標を文字を使って表すとき、「x,y はさけて」おきます。
これは、代入したものかどうかが分からず、混乱をしてしまう可能性があるためです。
そのため、x,y をさけますし、直線の式を表すときに使う a,b もさけて使いましょう。
一般的には、s, t などを使って表すことが多いです。
＜まとめ＞
・座標が決まっていない点を考えるときは、「x座標を文字でおく」といい
・問題の条件を読み取り、「どのように設定していけばいいのか」を考える
・点がグラフ上（直線上）にあるのなら、x座標が分かればy座標が分かる
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|
