（１）連立方程式の解とグラフ
連立方程式の解は、「各方程式のグラフの交点」として表せます。

【例題】
連立方程式　x＋2y＝6…①、2x－y＝2…②　の解を求めなさい。

この連立方程式①・②を、それぞれ「yについて解く」と、

・x＋2y＝6
2y＝－x＋6
y＝－(1/2)x＋3…①

・2x－y＝2
－y＝－2x＋2
y＝2x－2…②

①、②をグラフに表すと、このようになります。

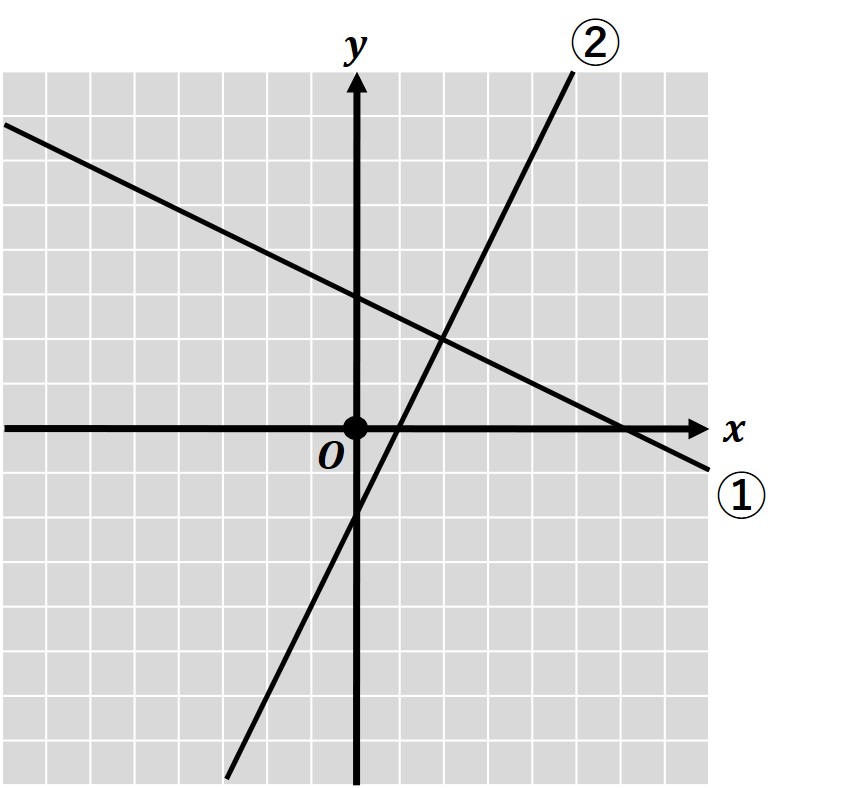
すると、２つのグラフが(2, 2)で交わり、これは連立方程式の解と一致します。
つまり、〔連立方程式の解〕＝〔一次関数のグラフの交点〕ということです。
 
 
（２）一次関数のグラフの交点
「グラフの交点の座標」は、連立方程式を解いて求めることができます。
これは、上の（１）で解いた内容そのままが理由です。

そのため、「一次関数のグラフの交点は連立方程式を解いて求めればいい」ということになります。

〔例題〕次の一次関数のグラフの交点を求めなさい。
y＝－(1/2)x＋3…①
y＝2x－2…②

連立方程式の解を出すことになるのですが、代入法で解きましょう。
（加減法で解くために、文字を左辺へ移項すると時間がかかるため）

①を②に代入すると
－(1/2)x＋3＝2x－2
－x＋6＝4x－4
－5x＝－10
x＝2
これを②に代入すると
y＝2・2－2＝2

したがって、x＝2, y＝2
これが交点の座標なので、交点は(2,2)

＜補足＞

グラフの交点を求めるときには、「交点がどの位置にあるのか」を確認しておきましょう。
交点の位置から、x, yの符号を確認しておくだけでも、計算ミスをしたときに気付くきっかけになる可能性があるからです。

そのため、簡単なものでいいので、一次関数のグラフをかいて求めるようにしましょう。

＜まとめ＞

・連立方程式の解は、「各方程式のグラフの交点」として表せる
・「グラフの交点の座標」は、連立方程式を解いて求めることができる
・連立方程式を解いて交点の座標を求めるときは、代入法で解くとよい