（１）方程式をグラフに描く
ax＋by＋c＝0（a,b,cは定数）のグラフは直線となります。
なぜなら、yについて見れば、1次式なので、y＝〇x＋●の形に変形できるからです。

たとえば、「方程式 2x－3y－6＝0 のグラフを描きなさい。」という問題なら、

2x－3y－6＝0
これをyについて解くと、
－3y＝－2x＋6
両辺を －3 で割ると
y＝(2/3)x－2
と変形できます。

つまり、方程式 2x－3y－6＝0 のグラフは、「傾きが 2/3 で、切片が －2 の一次関数のグラフ」であるということです。
 
 
（２）「x＝〇」「y＝〇」のグラフ
「x＝〇のグラフはy軸に平行」になり、「y＝〇のグラフはx軸に平行」になります。

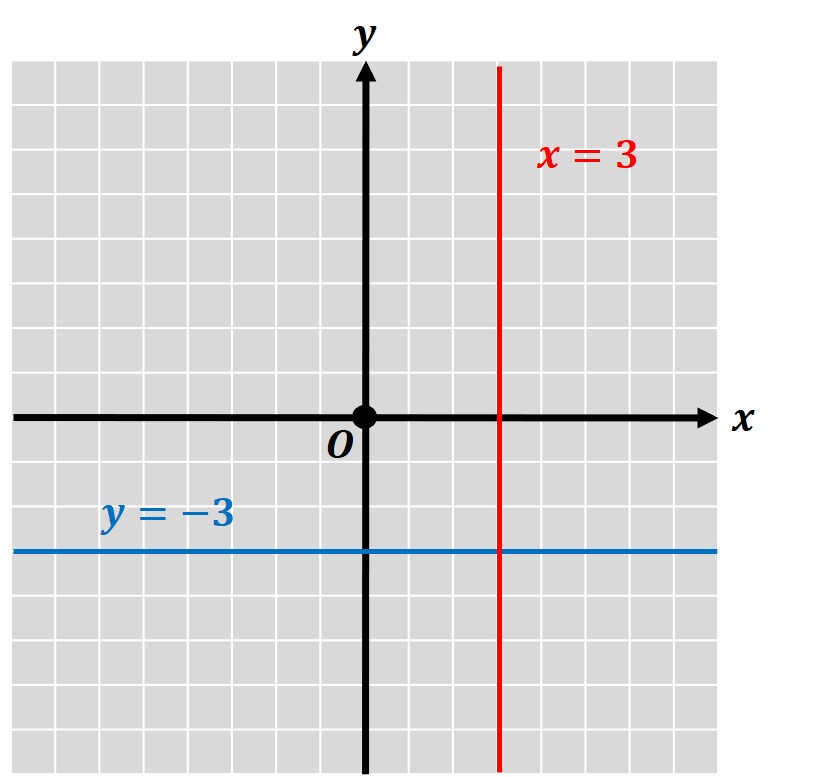
たとえば、「x＝3」をグラフに表そうとします。
この式は「yはおらず、x＝3だけ」が示されていますので、「yの値に関係なく、常にx＝3である」ことをグラフとして表せばいいということです。

同様に、「y＝－3」のグラフであれば、「xの値に関係なく、常にy＝－3である」ことをグラフとして表せばいいということです。

これらを座標軸上に表すと、以下のようになります。

＜補足＞

「方程式 2x－3y－6＝0 のグラフを描きなさい。」の別解として、「x＝0 や y＝0 を代入」して通る点を見つける方法もあります。

x＝0 を代入すると、y＝2
y＝0 を代入すると、x＝3

このことから、 2x－3y－6＝0 のグラフは (0, 2)と(3, 0)を通るグラフである、と考えることができます。
どちらの方法でも結果は同じですので、解きやすい方法で慣れておきましょう。

＜まとめ＞

・方程式 ax＋by＋c＝0 のグラフは直線となる
・「方程式 ax＋by＋c＝0」を y について解くと、1次関数の式となる
・「x＝〇のグラフはy軸に平行」になり、「y＝〇のグラフはx軸に平行」になる