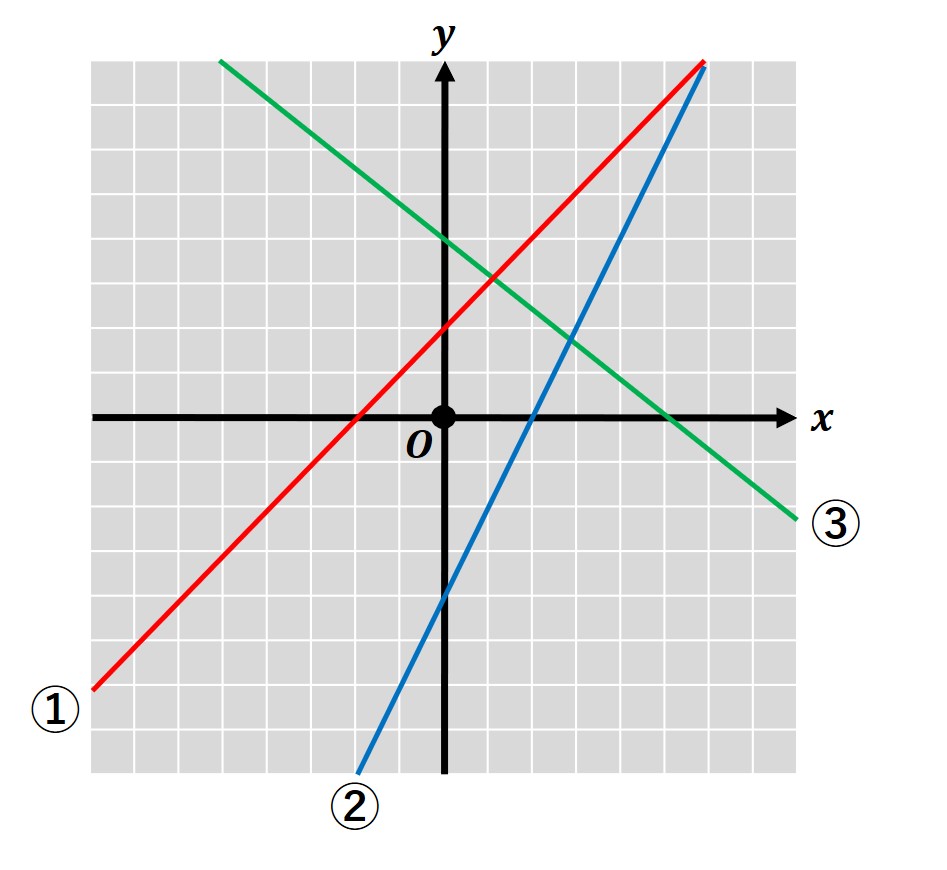
1次関数のグラフから、「1次関数の式を求める」手順はこのようになります。
（例として、赤いグラフ①の式を求めていきます）

〔手順１〕グラフから切片を求める（bの値を調べる）
まず、グラフから一目で読み取ることができるのは「切片」です。
こちらの値を読み取ると、y＝ax＋b の b の部分が分かります。

①であれば、y軸と(0,2)で交わっていますので、b＝2
つまり、①の式は y＝ax＋2 となります。
 
 
〔手順２〕x,yがともに整数となっている点を2つ見つけて、傾きを求める
次に、x,yがともに整数となっている点を2つ見つけます。
（そのうち、1つは切片で構いません）

そして、その2点について、「左側の点から右側の点を見た」場合に、
「右にいくつ増え、上にいくつ増えたのか」を調べます。
（右下がりのグラフの場合、－をつけて表現します）

①であれば、切片(0,2)と(1,3)を通っていますので、
「右に1増えると、上に1増える」と判断できます。
よって、傾き＝〔yの増加量〕/〔xの増加量〕＝上に〇 / 右に●で求めることができますので、
傾き＝1/1＝1　つまり a＝1 となります。
 
 
〔手順３〕求めた傾き・切片から、式をつくる
上記の手順１・２より、a＝1（傾き）, b＝2（切片） と分かったので、
①のグラフは y＝x＋2 とわかります。
 
 
その他の②、③も同様に求めると、

②：切片＝－4，傾き＝2/1＝2 より、y＝2x－4
③：切片＝4，傾き＝(－4)/5＝－(4/5) より、y＝－(4/5)x＋4

＜まとめ＞

・〔手順１〕グラフから切片を求める（bの値を調べる）
・〔手順２〕x,yがともに整数となっている点を2つ見つけて、傾きを求める
・〔手順３〕求めた傾き・切片から、式をつくる