しかし、切片（y＝ax＋b の b ）が分数（や小数）である場合、正確な点をy軸上にとることはできません。
そこで、x,y ともに整数となる点を探します。

たとえば、y＝(3/5)x－(1/5)の場合、
両辺を5倍すると、5y＝3x−1 となります。
これを満たす x,y の組を探すと、x＝2, y＝1 と分かります。

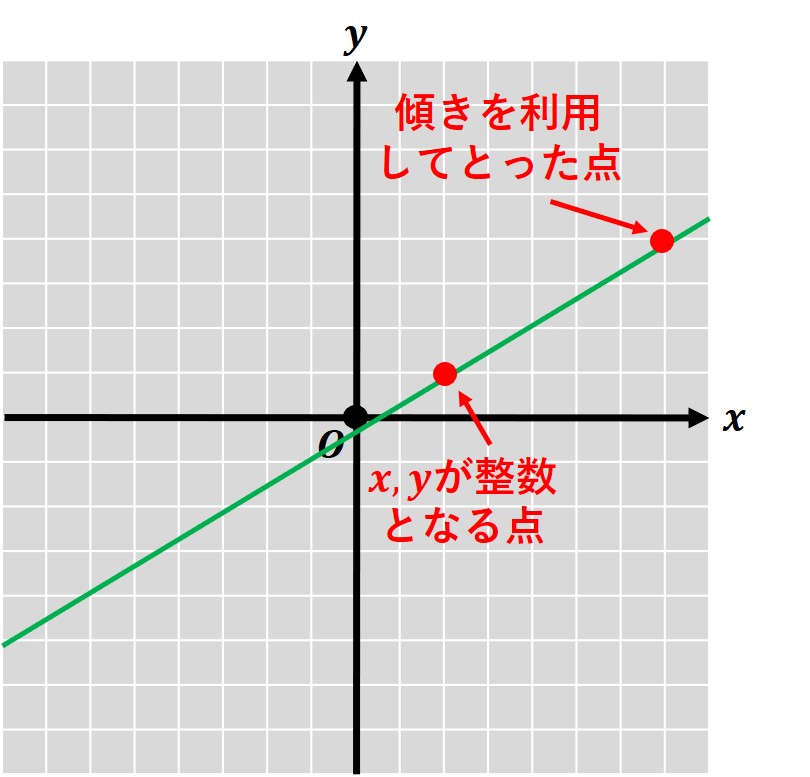
つまり、y＝(3/5)x－(1/5) のグラフは (2, 1)を通ることになります。
この (2, 1)から、傾きを利用して、
傾き 3/5 ⇒右に5進んだとき、上に3進むということから、
(2＋5, 1＋3)＝ (7, 4)を通ることが分かります。

これらのことから、
y＝(3/5)x－(1/5) のグラフは、 (2, 1)と (7, 4)を通ることになります。
あとは、この2点を結んであげればグラフは完成です。

＜補足＞

今回、y＝(3/5)x－(1/5) のグラフが通る格子点（x,y座標ともに整数である点）を探すために、
両辺を5倍して　5y＝3x−1 としました。
必ずしも、この方法でなくても構いません。

y＝(3/5)x－(1/5)＝(3x－1)/5　とすると、「3x－1 が 5の倍数であるとき、yが整数になる」ことが分かります。このように、考えることもできますので、自分なりの近道を色々と試してみてください。

＜まとめ＞

・y＝ax＋b の「bが整数でない」場合、そのままでは正しいグラフがを描けない
・y＝ax＋b の「bが整数でない」場合、x,y ともに整数となる点を探す
・取った切片から、傾きを考慮して、もう1点とる