| 〔質問〕 正四面体OABCで頂点Oから平面ABCに下ろした垂線の足をHとすると点Hが△ABCの重心になるのはなぜですか? |
| 〔回答〕 重心になるというよりは「外心になるから」というのが直接的な理由です。 そして、正三角形ですので、「外心」=「重心」という流れです。 理由は下記を読んでください! 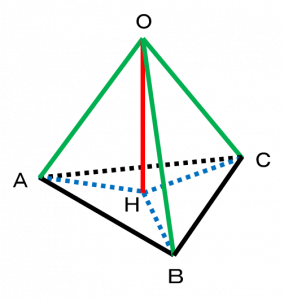 このときの、△OAH と △OBH と △OCH について考えてみると、 まず、OH は底面に垂直ですから、3つの三角形とも直角三角形ということになります。 次に、これは正四面体ですから、OA=OB=OC で、さらにすべて OH は共通ですから、 よって、この3つの三角形は合同ということになり、AH=BH=CH が言えます。 これはつまり、点H が △ABC の外心であるということになり(各頂点までの距離が等しいので、外接円が書ける)、正三角形ですので重心と一致している、ということです。 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |


