| 〔質問〕 「AP+BP を最短にする P を直線L上に見つける問題」の手順を教えてください。 |
| 〔回答〕 理科の「鏡における光の反射」をイメージしてください。同じ考え方で大丈夫です! 直線について、点Bと対称な点B’をとります。 その点B’と点Aを結んだ直線と、直線lとの交点がPとなります。 (点Aの方を反対側に移しても構いません) 理由は以下の図を参照してください そもそも、直線に対して対称な点をとったときに、直線上の点Pがどこにあろうと、必ず BP=BP’ という関係があります(対称な点をとれば二等辺三角形PBB’ができるはずなので)。 ということは、「AP+BP の最短を求める」というのを「AP+B’P の最短を求める」に読み替えることができます。 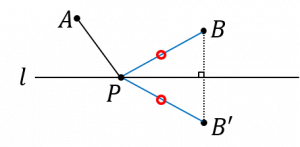 そして「AP+B’P の最短」については、遠回りせず直線的に進めば最短のはずですから、求めるべき個所は「線分AB’上」ということになります 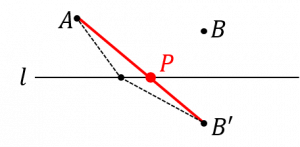 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

