<ポイント>
・直線上にある点は、その座標を直線の式に代入したとき、式が成り立つ
・求めたい1次関数のグラフが通っている2点の座標が分かれば、式は求められる
・「グラフが通っている2点の座標」から、そのグラフの傾きを求める
3点 A(-2, 1), B(4, 10), C(a, a+1)がある。この3点A, B, C が一直線上にあるような a の値を求めなさい。
【解説】
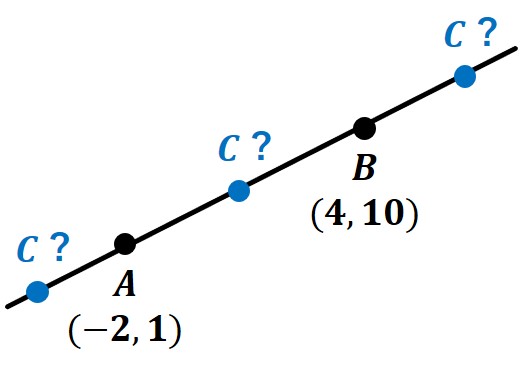
点Cの座標が分からないため、Aより左か右か…
それすら分からない状況です。
しかし、「点Cは直線AB上にある」ということから、直線ABの式にCの座標(a, a+1)を代入すると成り立つ、ということになります。
つまり、直線ABの式を求めて、その式に(a, a+1)を代入すればよい、ということです。
(求めたい1次関数のグラフが通っている2点の座標が分かれば、式は求められる)
「グラフが通っている2点の座標」から、そのグラフの傾きを求めると、
〔ABの傾き〕=9/6=3/2
よって、ABの式は y=(3/2)x+b という形になります。
これにB(4, 10)を代入すると、
(3/2)・4+b=10
6+b=10
b=4
したがって、直線ABの式は y=(3/2)x+4 だと分かります。
これに、C(a, a+1)を代入して、
(3/2)a+4=a+1
(1/2)a=-3
a=-6 (答え)
<まとめ>
・直線上にある点は、その座標を直線の式に代入したとき、式が成り立つ
・求めたい1次関数のグラフが通っている2点の座標が分かれば、式は求められる
・「グラフが通っている2点の座標」から、そのグラフの傾きを求める
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

