<ポイント>
・2直線の交点の座標は「連立方程式の解」となる
・三角形の面積を二等分する場合は「底辺を二等分して、高さの等しい三角形を2つつくる」と考える
・「底辺を二等分する点」は「底辺の両端となる2点の中点」
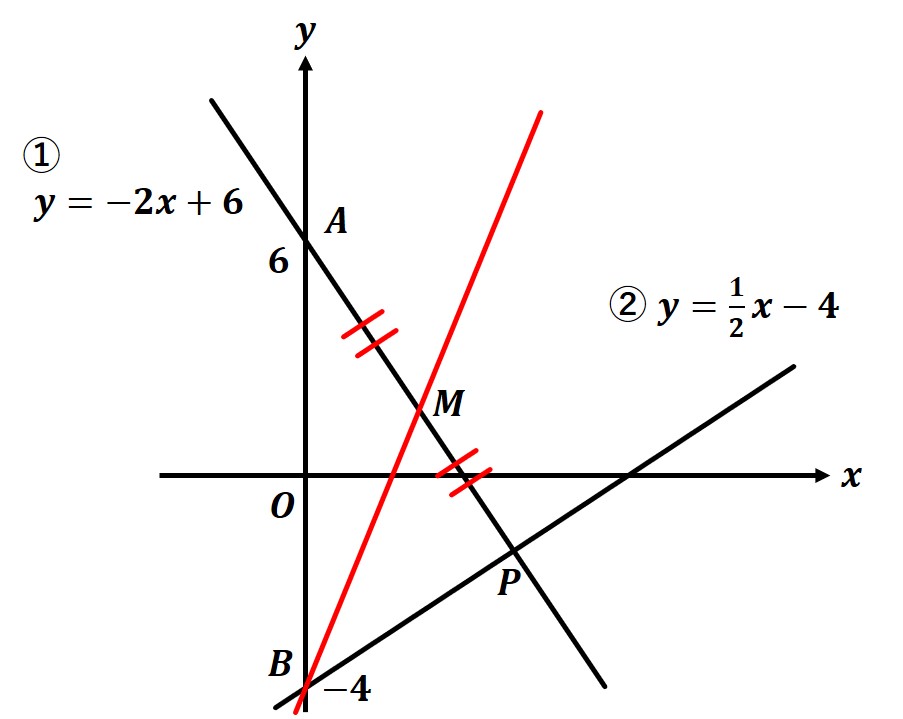
図のように、2つの直線 y=-2x+6…① と、y=(1/2)x-4…②があります。①、②の交点をPとし、x軸と①の交点をA、x軸と②の交点をBとします。このとき、点Bを通り、△ABPの面積を二等分する直線の式を求めなさい。

【解説】
まず、△ABPの面積を「点Bを通る直線が二等分する」ためには、その直線がどのような点を通ればよいのかを考えます。
たとえば、辺の長さが分かっているのなら、その辺の長さを用いて実際の面積を計算していくことができますが、座標平面上では難しいです。
そこで、座標平面上において三角形の面積を二等分する場合は「底辺を二等分して、高さの等しい三角形を2つつくる」と考えればよいです。
△ABPのAPを底辺として考えると、これを二等分する点は2点A,Pの中点Mとなります。
(この中点Mの座標は、「2点A,Pの座標の平均」というようにイメージしましょう)
そして、中点Mの座標が分かれば、求める直線は「2点B,Mを通る直線」となるので、この式を求める流れになります。
まずは、点Pの座標から求めていきます。
点Pは2直線①、②の交点なので、①、②の「連立方程式の解」を求めます。
・y=-2x+6…①
・y=(1/2)x-4…②
これを解いて、x=4, y=-2
つまり、Pの座標は(4, -2)と分かります。
そして、2点A, Pの中点Mの座標を求めていくと、
・Mのx座標=(0+4)/2=2
・Mのy座標=(6-2)/2=2
よって、Mの座標は(2, 2)となります。
あとは、2点 B(0, -4)とM(2, 2)を通る直線の式を求めていきます。
〔BMの傾き〕=6/2=3 と分かり、〔切片〕=-4(Bのy座標)
求める式は y=3x-4 (答え)
<まとめ>
・2直線の交点の座標は「連立方程式の解」となる
・三角形の面積を二等分する場合は「底辺を二等分して、高さの等しい三角形を2つつくる」と考える
・「底辺を二等分する点」は「底辺の両端となる2点の中点」
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

