〔質問〕

微分の問題で、増減表からグラフを書く時に傾きが0であるためになのかはよく分からないのですが、交点ではなく接点であるためにグラフを少しグネッと書くことがあると思うのですが、それはなぜなのですか？
またどのように書けば採点者に伝わるのですか？

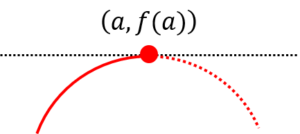
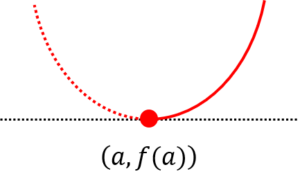
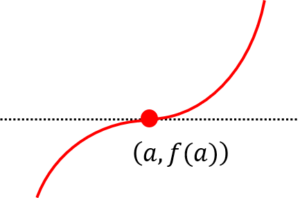
〔回答〕

一続きではなく、f'(x)＝0 となる箇所の前後で分けて考えてみてください。
※ 特殊なことが起こっているというわけではないです。

（以下、導関数が「＋→0→＋」の場合について記載します）

まず、それまで（x＜a）というのは、導関数の値（接線の傾き）が、
・正で
・段々と減っている
という状況になっていると思いますので、
以下の図のような形で (a, f(a)) の箇所に向かいます。

書き方のコツとしては、「図の点線（赤）までをイメージしながら書きつつ、その途中でやめる（実線部分を残す）」という感じです。

 
次に、それ以降（x＞a）については、導関数の値（接線の傾き）が、
・正で
・（少なくとも多少は）段々と増えていく
という状況になっていると思いますので、
以下のような形で (a, f(a)) の箇所から離れていきます。

こちらも「点線（赤）からをイメージしながら、途中から書く」という感じです。

 
実際に点線部分はありませんから、これらを繋げると、このような形状になる、というものです。
これらのことを意識しておけば、答案上は問題なく書けていると思います。