（１）2つの三角形が「合同である」と言えるのは
2つの三角形が「合同である」ということを言うには、「3つの合同条件」のうち、いずれかに該当すれば言うことができます。

・合同条件①：3組の辺がそれぞれ等しい
・合同条件②：2組の辺とその間の角がそれぞれ等しい
・合同条件③：1組の辺とその両端の角がそれぞれ等しい

これらのうち、どれでも構わないので、問題で与えられた条件の中から言うことができれば、
「2つの図形は合同である」と判断できます。
（見た目だけで、「たぶん合同だろう」というのはダメです）
 
 
（２）合同条件①：3組の辺がそれぞれ等しい
（こちらの図において、同じ色の辺・角は等しいものとする）

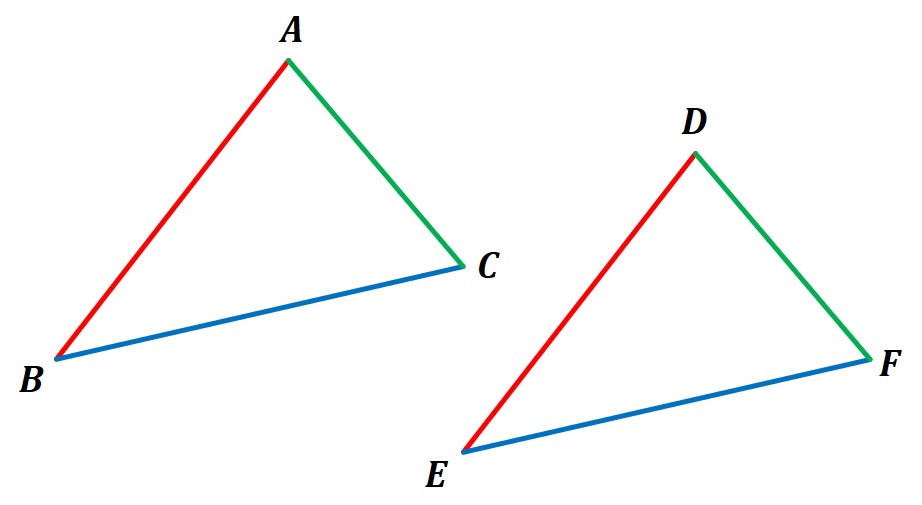
この図のように、AB＝DE、BC＝EF、CA＝FD という関係になっていれば、

「合同条件①：3組の辺がそれぞれ等しい」が成り立ち、合同であると判断できます。
 
 
（３）合同条件②：2組の辺とその間の角がそれぞれ等しい
（こちらの図において、同じ色の辺・角は等しいものとする）

この図のように、AB＝DE、BC＝EF、∠ABC＝∠DEF という関係になっていれば、

「合同条件②：2組の辺とその間の角がそれぞれ等しい」が成り立ち、合同であると判断できます。
 
 
（４）合同条件③：1組の辺とその両端の角がそれぞれ等しい
（こちらの図において、同じ色の辺・角は等しいものとする）

この図のように、BC＝EF、∠ABC＝∠DEF、∠ACB＝∠DFE という関係になっていれば、

「合同条件③：1組の辺とその両端の角がそれぞれ等しい」が成り立ち、合同であると判断できます。

＜補足＞

３つの合同条件は、必ず教科書通りに正しく覚えておきましょう。
このあとにする「証明」の問題では、正しく書かないと減点対象となります。

＜まとめ＞

・合同条件①：3組の辺がそれぞれ等しい
・合同条件②：2組の辺とその間の角がそれぞれ等しい
・合同条件③：1組の辺とその両端の角がそれぞれ等しい