<ポイント>
・ある立体を「一定の割合で拡大・縮小した立体」は、もとの立体と相似である
・相似比 a:b ⇒ 体積比 a3:b3
・円すい台の体積は、〔大きい円すい〕-〔小さい円すい〕で求める
図のように、円すいを底面に平行な平面で切り取り、高さが3等分になるように3つの立体に分けました。真ん中の立体の体積が28πであるとき、一番下の立体の体積を求めなさい。
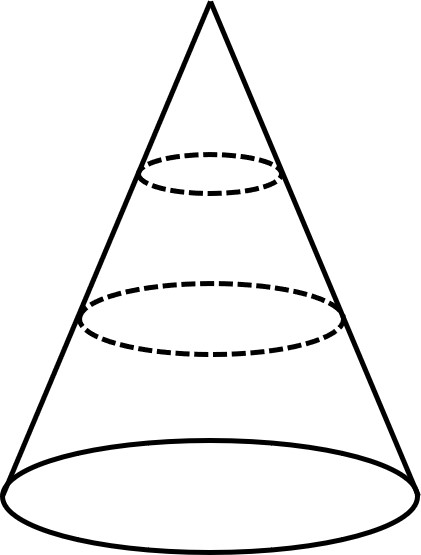
【解説】

問題より「底面に平行な平面で3等分した」とありますので、
上の図の〔Aの円すい〕・〔A+Bの円すい〕・〔A + B + Cの円すい〕は相似と言えます。
(それぞれの展開図において、側面の中心角が等しく、底面の円が相似)
〔Aの円すい〕・〔A+Bの円すい〕・〔A + B + Cの円すい〕の相似比は、
高さの関係から、〔Aの円すい〕:〔A+Bの円すい〕:〔A + B + Cの円すい〕=1:2:3
ということです。
この図を用いて、A・B・Cそれぞれの部分の体積を考えていきます。
相似比〔Aの円すい〕:〔A+Bの円すい〕:〔A + B + Cの円すい〕=1:2:3 より、
体積比は 13:23:3 3=1:8:27 となります。
BやCなどの円すい台の体積は、〔大きい円すい〕-〔小さい円すい〕で求めます。
(直接的に求めることはできない)
よって、
Aの部分=1
Bの部分=(A+B)-A=8-1=7
Cの部分=(A+B+C)-(A+B)=27-8=19
よって、Cの部分は「全体27のうち、19がある」ということになります。
そして、問題で与えられているBの部分と比べると、体積比は 7:19 になるので、
〔Cの部分の体積〕=〔Bの体積〕・(19/7)=28π・(19/7)=76π (答え)
<まとめ>
・ある立体を「一定の割合で拡大・縮小した立体」は、もとの立体と相似である
・相似比 a:b ⇒ 体積比 a3:b3
・円すい台の体積は、〔大きい円すい〕-〔小さい円すい〕で求める
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|


