このとき、
ABとDC、BEとCE、EAとEDはそれぞれ対応する辺となっています。
たとえば、
AB：DC＝2：1であれば、BE：CE＝EA：ED＝2：1となっているということ。
（相似な図形の性質より）

このような、「対応する辺の比」のことを相似比といいます。
「相似比が2：1である」図形の辺の比は、どの対応する辺の比を見ても2：1となっています。
 
 
（２）相似の中心
相似な図形の対応する点を通る直線を結ぶと１点で交わります。
このとき、（相似な）２つの図形は「相似の位置にある」といいます。

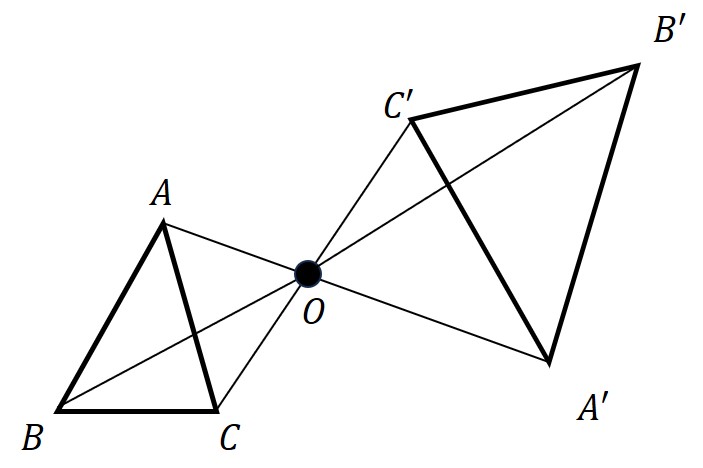
この、「相似な図形の対応する点を通る直線の交点」を相似の中心といいます。
上の図の場合は「点Oが相似の中心」ということになります。

「相似の中心から、それぞれの対応する点までの距離の比は等しい」ので、
OA：OA’＝OB：OB’＝OC：OC’　となっています。

＜補足＞

「相似比が1：1」である２つの図形は、合同です。

合同な図形は、すべての辺の長さが同じなので、どの対応する辺の比を見ても1：1になっています。

＜まとめ＞

・相似な図形で「対応する線分の長さの比」を相似比という
・相似な図形の対応する点を通る直線を結ぶと１点で交わる（相似の位置）
・相似な図形の対応する点を通る直線の交点を相似の中心という