（１）根号を含む式の除法
根号（√ ）を含む式の除法は、まず「√ の中の数を小さくしてから」計算を始めます。

わり算をすることで、√ の数が小さくなりますが、あらかじめしておいた方が約分しやすくなります。a√b の形にするのに時間がかかったり、ミスが起こりやすくなるためです。
どのような計算においても同じことが言えますが、できるだけ「小さな数で」計算するように心がけてください。

√ の中の数を小さくしたら、ひとつの根号（√ ）の中にまとめて計算します。

なお、除法が混じった計算では、必要に応じて最後に有理化する必要があります。
分母に √ が残った状態で答えにしては、減点もしくは不正解となるので気をつけましょう。

【根号を含む式の乗除の法則】
・√a × √b＝√(a・b)
・√a ÷ √b＝√a / √b＝√(a/b)
 
 
【例題１】
(3√2) ÷ (√24)
 
 
【解説１】
(3√2) ÷ (√24)
＝ (3√2) ÷ (2√6)　（←√ の中を小さくする）
＝ (3√2) /{(2√(2×3)}　（←√ の中を素因数分解しておく）
＝ (3√2) /{2×(√2)×(√3)}　（← √2 どうしで約分する）
＝ 3 / (2√3)
＝ {3×(√3)} / {(2√3)×(√3)}　（← √3 をかけて有理化）
＝ (3√3) / 6　（← 3で約分する）
＝ (√3) / 2
 
 
（２）根号を含み、乗除が混じった計算
根号を含み、乗除が混じった計算では、「大きく√ をとって、その中で計算する」ことで約分をする機会が増えます。

【例題２】
－(√50) ×(√24)÷ (5√3)
 
 
【解説２】
－(√50) ×(√24)÷ (5√3)　は、乗除を含む計算ですので、
「大きく√ をとって、その中で計算する」ことで約分をしてみます。

その際、 (5√3)＝√75 と、あえて大きくすると、約分しやすくなります。
（今回の場合、√50 があるので、25で約分できそう）

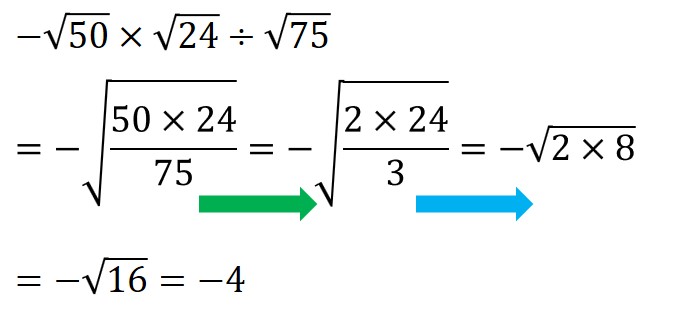
√の中でひとまとめにし、
緑色の矢印「25で約分」、青色の矢印「3で約分」
をすると、√ の中が 16 とかなり小さくなりました。

このように、約分できそうな部分を見つけて、どんどん数を小さくして計算していきましょう。

＜まとめ＞

・√a × √b＝√(a・b) / √a ÷ √b＝√a / √b＝√(a/b)
・除法が混じった計算では、必要に応じて最後に有理化する必要がある
・乗除が混じった計算では、「大きく√ をとって、その中で計算する」