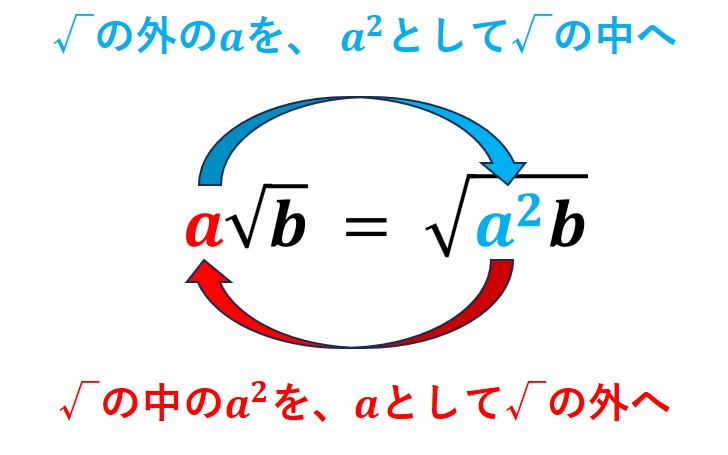
（１）√の外の a を、a² として√の中へ入れる
√の外の a を、a² として√の中へ入れることができます。

式にすると、a√b＝√(a²・b) ということです。

これは、a√b＝a・√b＝√(a²)・√b＝√(a²・b)
と変形できるためです。

【例】次の数を、√a の形で表しなさい。
① 2√2＝ √(2²・2)＝√8

② 6√5＝√(6²・5)＝√180

③ (√28) / 2＝ √28 / √4＝√(28/4)＝√7
 
 
（２）√の中の a² を、a として√の外へ出す
√の中の a² を、a として√の外へ出すことができます。
その結果、「√の中の数が小さくなり、計算しやすく」なります。
そのためには、「√の中の数を素因数分解して、2乗を見つける」ことが必要です。

式にすると、√(a²・b)＝a√b　ということです。

これは、√(a²・b)＝(√a²)・√b＝a・√b＝a√b
と変形できるためです。

【例】次の数を、a√b の形で表しなさい。
① √12＝√(2²・3)＝2√3

② √45＝√(3²・5)＝3√5

③ √0.24＝√(24/100)＝√24 / √100
　＝√(2²・6) / √(10²)
　＝(2√6) / 10＝(√6) / 5
（√の外にある数どうしは、約分できる）

＜補足＞

（２）の「√の中の a² を、a として√の外へ出す」という作業は、非常に大切です。
「√の中の数が小さくなり、計算しやすく」なるからです。特に、乗法（かけ算）をする場合や、加法・減法（たし算・ひき算）のときには重要です。

そのため、こちらの練習は必ず積んでおきましょう。
目標は、「できるだけ、素因数分解の筆算をせずとも、√の中身を小さくできる」ということです。

＜まとめ＞

・a√b＝√(a²・b)（√ の前につく数を、√の中に入れる）
・√(a²・b)＝a√b（√の中の数を小さくする）
・√の中身を小さくするには、「√の中の数を素因数分解して、2乗を見つける」ことが必要