（１）展開する
単項式や多項式の積を、「単項式の和の形」にすることを展開するといいます。

－2(－2x＋6) ＝ (－2)・(－2x)＋(－2)・6 ＝ 4x－12

このように、分配法則を使って（　　）をはずす作業も、「展開」です。
 
 
（２）多項式どうしの乗法
多項式どうしの乗法では、このような順で展開していきます。

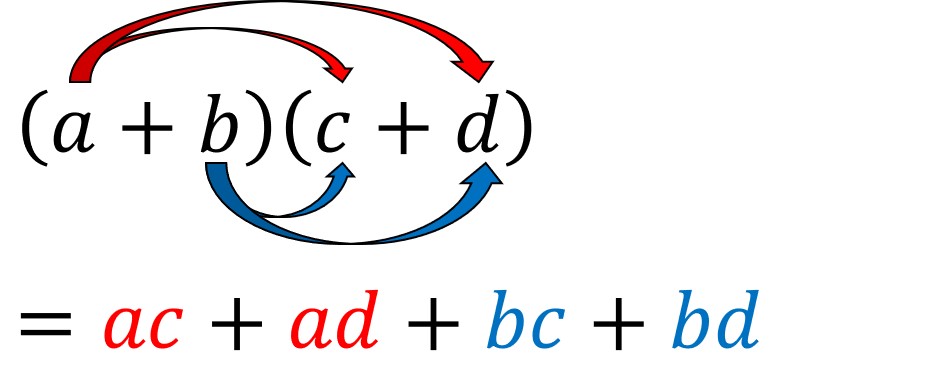
ふつう、左側にある多項式のはじめの項から順に、右側の項とのかけ算（展開）をしていきます。
（この図では、赤のかけ算、青のかけ算の順になる）

そして、展開が終われば、同類項をまとめて計算が終わります。
 
 
〔例〕
① (x＋a)(y＋b)
＝x・y＋x・b＋a・y ＋a・b
＝xy＋bx＋ay＋ab

② (2x＋5)(3y−1)
＝ 2x・3y−2x・1＋5・3y−5・1
＝ 6xy−2x＋15y−5

③ (x＋y)(4x＋3y)
＝ x・2x＋x・3y＋y・4x＋y・3y
＝ 2x²＋3xy＋4xy＋3y²　（同類項があればまとめる）
＝ 2x²＋7xy＋3y²

④ (2x＋y)(x＋5y)
＝2x・x＋2x・5y＋y・x＋y・5y
＝2x²＋10xy＋xy＋5y²　（同類項があればまとめる）
＝2x²＋11xy＋5y²

＜まとめ＞

・単項式や多項式の積を、「単項式の和の形」にすることを展開するという
・〔多項式の展開〕(a＋b)(c＋d)＝ac＋ad＋bc＋bd
・展開したあと、同類項をまとめる