【例題】
5本のうち3本があたりである「くじ」がある。そこから先にAが1本をひき、それを戻さずにBも1本ひくとき、それぞれあたりをひく確率を求めなさい。
 
 
【解説】

まずは、Aがあたりをひく確率を考えると、
「5本のうち3本があたり」なので、3/5 と分かります。

次に、Bがあたりをひく確率を考えるのですが、まずは〔すべての場合の数〕を求めます。

A,Bが連続してくじをひくとき、
Aのひき方は5通り、Bのひき方は4通りとなります。
（Bがひくとき、Aが1本ひいた後になるため）

よって、〔すべての場合の数〕＝5×4＝20通り

ここから、5本のくじに名前をつけて考えます。
①②③をあたりくじ、④⑤をはずれくじとすると、

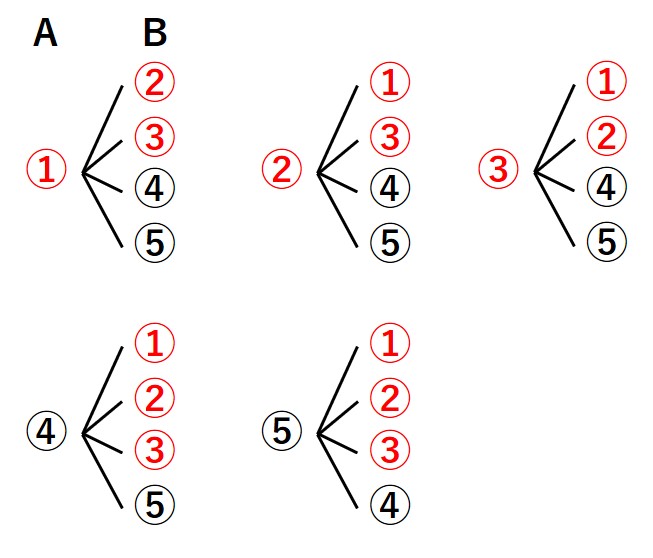
（Aのひいたくじ, Bのひいたくじ）として、Bがあたる場合を書き出すと、
（①, ②）, （①, ③）
（②, ①）, （②, ③）
（③, ①）, （③, ②）
（④, ①）, （④, ②）, （④, ③）
（⑤, ①）, （⑤, ②）, （⑤, ③）
これら、12通りのあたりのひき方があります。

よって、Bがあたりをひく確率は、12/20＝3/5

答え　Aがあたりをひく確率… 3/5, Bがあたりをひく確率… 3/5

このように、二人でくじをひく場合は、先にひく人の方が有利に思えますが、あたる確率は同じになります。
この結果を覚えておくと便利です。

＜補足＞

あたりくじをひく場合を抽出して書き出しましたが、数え漏れが出るかも…と自信がない場合は樹形図を使って考えると分かりやすいと思います。

＜まとめ＞

・確率を求めるときは、まず「すべての場合の数」を求める
・区別がないものでも、確率を考えやすくするため名前をつけると便利
・二人でくじをひく場合は、あたる確率は同じになる