【例題】
袋の中に、赤玉が3個、黒玉が2個入っています。この中から、同時に2個の玉を取り出すとき、次の確率を求めなさい。

① 2個とも赤玉になる確率
② 1個が赤、1個が黒になる確率

【解説】

赤玉、黒玉の中では、それぞれ区別がありません。（見た目から判断できない）
考えやすくするために、赤玉を①②③、黒玉を④⑤として考えると表しやすくなります。
（①～⑤などの数字でなくても、A～Eなどのアルファベットでも構いません）

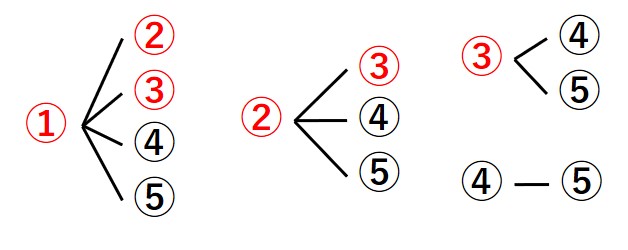
まず、〔すべての場合の数〕を求めます。

（1, 2）, （1, 3）, （1, 4）, （1,5）
（2, 3）, （2, 4）, （2, 5）
（3, 4）, （3, 5）
（4, 5）
の10通りある。

① 2個とも赤玉になる確率
「2個とも赤玉になる」ということは、「①〜③のみ」を使う組み合わせを選べばいい。

よって、（①, ②）, （①, ③）, （②, ③）の3通り。
したがって、3/10（答え）
 
 
② 1個が赤、1個が黒になる確率
「1個が赤、1個が黒になる」のは、
（①, ④）, （①, ⑤）, （②, ④）, （②, ⑤）, （③, ④）, （③, ⑤）の6通り。

したがって、6/10＝3/5（答え）

＜まとめ＞

・確率を求めるときは、まず「すべての場合の数」を求める
・区別がないものでも、確率を考えやすくするため名前をつけると便利
・書き出すときに樹形図を用いると、数え漏れしにくい