（１）平行四辺形になるための条件
「２つの三角形が合同である」ことや、「二等辺三角形である」ことを証明したように、「平行四辺形である」ことを証明することがあります。

平行四辺形になるための条件は５つあるので、すべて覚えておきましょう。

①２組の対辺がそれぞれ平行である（定義）
②２組の対辺がそれぞれ等しい
③２組の対角がそれぞれ等しい
④対角線がそれぞれの中点で交わる
⑤１組の対辺が平行でその長さが等しい

上記のように、条件は平行四辺形の定義や定理を用いたものになっています。

 
 
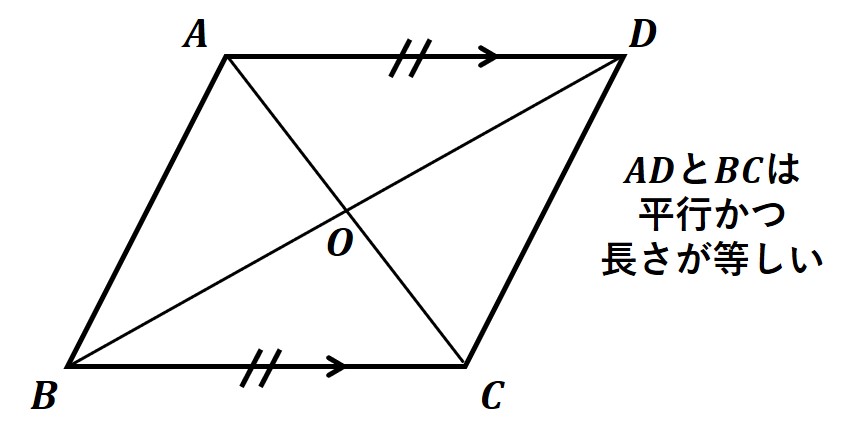
（２）平行四辺形であることの証明
平行四辺形であることを言うためには、「辺の長さが等しい」ことや「角の大きさが等しい」ことを言う必要があります。

そのため、あらかじめ平行四辺形の中にある「三角形の合同」を証明することがあります。
三角形の合同を証明することで「対応する辺や角が等しい」ということが使えます。

１つの証明の中に、２つの証明が入っているようなイメージです。

＜補足＞

平行四辺形であることを証明するために、三角形の合同の証明を使うことがあると紹介しました。

その他にも、平行四辺形の一辺を延長して、「外角を使う」こともあります。
日頃からさまざまなパターンを演習しておく（証明の練習をしておく）ことで気付きが増えるので、たくさんの問題に触れておくようにしましょう。

＜まとめ＞

・「平行四辺形である」ことを証明することがある
・平行四辺形の定義や定理を用いて、証明する
・平行四辺形であることの証明には、「三角形の合同を使う」ことがある