（１）定義
定義とは、「使うことばの意味をはっきりと述べたもの」です。
（そのことばの意味、と考えることもできます）

定義は「１つのことばに対して、１つだけ」あります。

〔定義の例〕
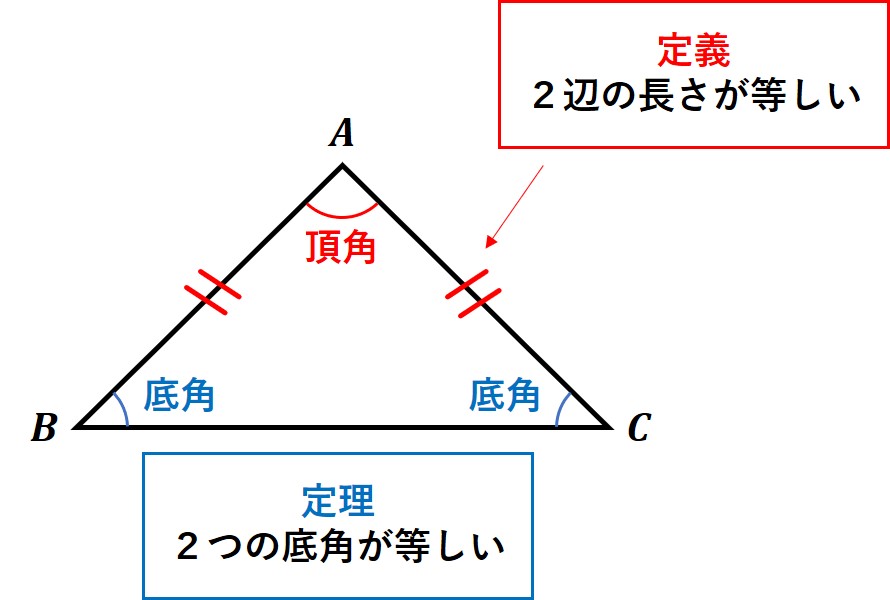
・二等辺三角形の定義
　「２つの辺の長さが等しい三角形」

・正三角形の定義
　「３つの辺の長さが等しい三角形」

・平行四辺形の定義
　「２組の対辺がそれぞれ平行な四角形」
 
 
（２）定理
定理とは、「証明された事柄のうち、重要なもののこと」です。

定義から導かれたものを、「性質」や「定理」といいます。
「特に大切な性質を述べたもの」を定理という、と考えてもらったら大丈夫です。

〔定理の例〕（性質も含みます）
・二等辺三角形の定理
　「２つの底角が等しい」「頂角の二等分線は、底辺を垂直に二等分する」

・正三角形の定理
　「３つ角が等しい（60°）」

・平行四辺形の定理
　「２組の対辺がそれぞれ等しい」「２組の対角がそれぞれ等しい」

このように、図形ごとに定理（性質）があります。

これらの定義・定理を使いながら、図形の証明を進めていくので、それぞれを正しく覚えておきましょう。

＜補足＞

＜まとめ＞

・「使うことばの意味をはっきりと述べたもの」を定義という
・「証明された事柄のうち、重要なもののこと」を定理という
・定義や定理にしたがって、証明を進めていく