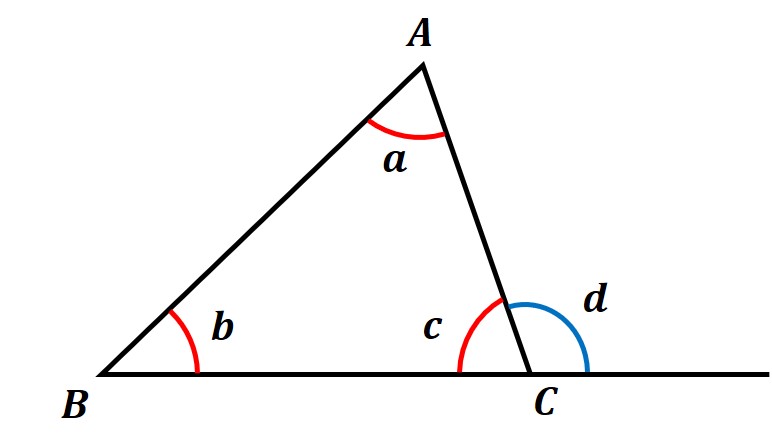
この図の∠a, ∠b, ∠c のように「多角形をつくる内部の角」を内角といいます。
内角の和は、その多角形が「何角形であるか」によって決まっていて、三角形の場合は180°です。
（∠a＋∠b＋∠c＝180°）

また、∠d のように「１辺とそのとなりの辺の延長とがつくる角」を外角といいます。
（こちらの図には表していませんが、∠a, ∠b のとなりにも、外角はあります）

 
 
（２）三角形の外角の性質
三角形の外角は「それととなり合わない２つの内角の和」に等しくなっています。

この図の三角形の外角 ∠d は、となり合う ∠c を除いた２つの内角 ∠a, ∠b
の和に等しくなっています。

式に表すと、∠d ＝ ∠a＋∠b ということです。
また、となり合う内角と外角の和は180°となっています。
（この図では、∠c＋∠d＝180°）

＜補足＞

なお、外角は「各頂点に対して２つ」できます。

この図でいえば、辺ACをCの方向に延長したとき、∠dの左下にできる角も外角となります。
そして、そのどちらの外角も大きさは等しくなっています。（対頂角の関係）

つまり、外角を考える場合は、その外角をつくるどちらの辺を延長して考えても、同じ大きさになるということです。

＜まとめ＞

・「多角形をつくる内部の角」を内角という
・多角形をつくる「１辺とそのとなりの辺の延長とがつくる角」を外角という
・三角形の外角は「それととなり合わない２つの内角の和に等しい」