（１）一次関数のグラフ
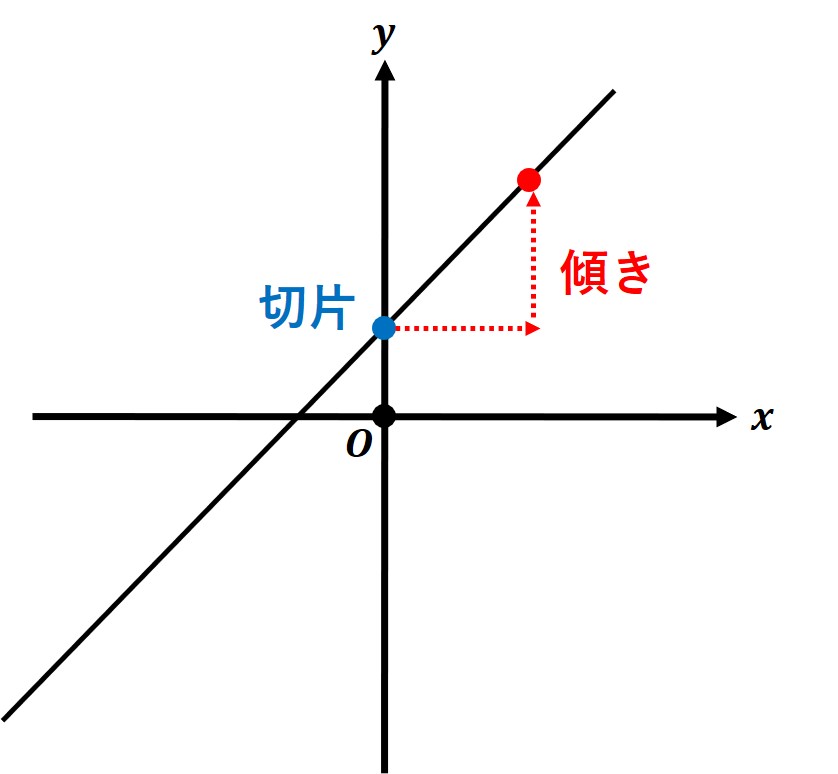
「一次関数 y＝ax＋b」の a を（グラフの）傾きといい、b を（グラフの）切片といいます。

つまり、式にある「a, bの値を見れば、どんなグラフになるのか分かる」ということです。

「aの値が傾き」を表しているので、「グラフがどんな傾きになっているのか」が分かり、
「bの値が切片」を表しているので、「グラフがどこでy軸と交わっているのか」が分かるようになっているのです。

これらを組み合わせることで、グラフを描いたり、描いてあるグラフを見て、式に表すことができます。

（２）一次関数 y＝ax＋b の a の符号
一次関数 y＝ax＋b の a の符号（正か負）を見るだけで、「そのグラフが右上がりか、右下がりか」が分かります。
y＝ax＋b の「a＞0（aは正） なら右上がり」「a＜0（aは負）なら右下がり」のグラフになります。

たとえば、
・y＝3x－5　なら、a＝3 で正の数なので、このグラフは右上がり
・y＝－2x＋1　なら、a＝－2 で負の数なので、このグラフは右下がり
と、判断できます。

＜補足＞

「b」が切片（y軸との交点となるy座標）となる理由は、「x＝0 を代入すると、b だけが残る」からです。y軸は x＝0 の直線であり、常にx座標が0となっているため、bだけ見れば「どの点でy軸と交わるのか」が分かる仕組みです。

＜まとめ＞

・一次関数 y＝ax＋b の a を（グラフの）傾きという
・一次関数 y＝ax＋b の b を（グラフの）切片という
・y＝ax＋b の「a＞0 なら右上がり」「a＜0 なら右下がり」のグラフになる