<ポイント>
・連立方程式には「解が無数にある」ものがある
・連立方程式には「解がない」ものがある
・「解が無数にある」「解がない」連立方程式の特徴を覚えること
〔問題〕次の連立方程式を解きなさい。
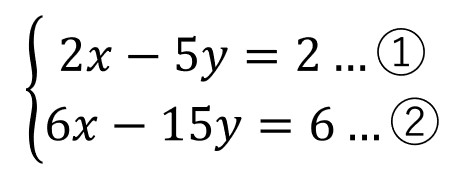
こちらの連立方程式を解こうとして、
①×3 をすると、6x-15y=6 となり、「②とまったく同じ式」となります。
これは、「①の解はすべて②でも成り立つ」ことになり、
そもそも①の解は無数にあります。
①:2x=5y+2 なので、
「x=7/2, y=1」, 「x=6, y=2」などがあります。
よって、この連立方程式の解は「無数にある」と言えます。
このような「解をもたない連立方程式」の特徴は、
「連立方程式の2つの式が、両辺ともに全く同じ」となるものといえます。
(2)「解がない」連立方程式
〔問題〕次の連立方程式を解きなさい。

こちらの連立方程式を解こうとして、
①×3 をすると、6x+15y=-6 となり、「②と(左辺)は同じなのに、(右辺)は異なる定数」となります。
仮に、この連立方程式の解があったとすれば、-6=6 となり、矛盾が起きることになります。
したがって、この連立方程式には「解がない」と言えます。
このような「解をもたない連立方程式」の特徴は、
「(左辺)または(右辺)はまったく同じ式」となるが、もう片方が異なるものといえます。
<まとめ>
・連立方程式には「解が無数にある」ものがある
・連立方程式には「解がない」ものがある
・「解が無数にある」「解がない」連立方程式の特徴を覚えること
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

