<ポイント>
・複合図形の体積・表面積を考えるときは「都合のいいように」分解して考える
・体積を考えるときは「[小さい円柱の体積]+[大きい円柱の体積]」
・表面積を考えるときは「真上から見た形」と「真下から見た形」が同じであることを利用する
【問題】
この図は、底面の直径が20で高さ10である円柱Aと、底面の直径が10で高さが5である円柱Bを組み合わせた立体図形です。
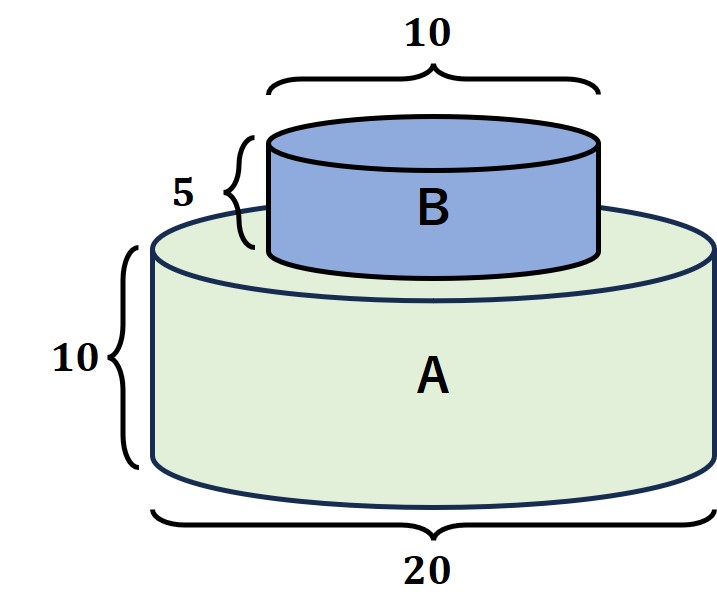
(1)この立体の体積を求めなさい。
(2)この立体の表面積を求めなさい。
【解説】
(1)この立体の体積を求めなさい。
体積を考えるときは「[小さい円柱の体積]+[大きい円柱の体積]」とすればよいので、
円柱A,Bそれぞれの体積を求めてあげればよい。
〔円柱Aの体積〕
〔円柱の体積 V〕=〔底面積(円) S〕×〔高さ h〕=〔πr2〕×〔高さ h〕なので、
π・102・10=100π・10=1000π
(直径が20なので、半径が10となることに注意)
〔円柱Bの体積〕
π・52・5=25π・5=125π
よって、
〔求める立体の体積〕=〔円柱Aの体積〕+〔円柱Bの体積〕
=1000π+125π
=1125π
(2)この立体の表面積を求めなさい。
表面積を考えるときは「真上から見た形」と「真下から見た形」が同じであることを利用します。
どちらから見ても、「半径10の円」に見えますので、この円2つ分を求めてあげます。
これに、〔立体の側面積〕=〔円柱Aの側面積〕+〔円柱Bの側面積〕を加えると解けます。
まずは、
〔上下からみた円の面積〕=π・102・2=100π・2=200π
(「2をかけた」のは、2つ分の面積を求めるため)
また、円柱A,Bの側面積を求めるには、それぞれの「底面の円周の長さ」を求めておく必要があります。
〔円柱Aの底面の円周〕=20π、〔円柱Bの底面の円周〕=10π
(円周の長さは、[直径] × π で求めます)
よって、
〔円柱Aの側面積〕=10・20π=200π
〔円柱Bの側面積〕=5・10π=50π
したがって、
〔立体の表面積〕=〔上下から見た円の面積〕+〔円柱Aの側面積〕+〔円柱Bの側面積〕
=200π+200π+50π
=450π
<まとめ>
・複合図形の体積・表面積を考えるときは「都合のいいように」分解して考える
・体積を考えるときは「[小さい円柱の体積]+[大きい円柱の体積]」
・表面積を考えるときは「真上から見た形」と「真下から見た形」が同じであることを利用する
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

