つまり、あるデータにおいて、
〔範囲(レンジ)〕＝〔最大値〕－〔最小値〕
ということです。

たとえば、

「下のデータは、A班の生徒の身長である。この範囲を求めなさい（単位は cm）」
A班　165.8　　171.4　　158.3　　181.2　　167.8　　175.9

ということであれば、この6人の身長の〔最大値〕〔最小値〕を見ると、
〔最大値〕＝181.2、〔最小値〕＝158.3　となっており、
〔範囲(レンジ)〕＝〔最大値〕－〔最小値〕　を用いて考えると、
〔範囲(レンジ)〕＝181.2－158.3＝22.9[cm]
 
 
（２）度数折れ線
「ヒストグラムの各長方形の上辺の中点を結んだグラフ」を度数折れ線といいます。
度数折れ線を書くときには、「左端は１つ前の階級の度数を0、右端は１つ先の階級の度数を0」とします。

こちらは、
「あるクラスの生徒40人の1週間の睡眠時間の度数分布表」です。

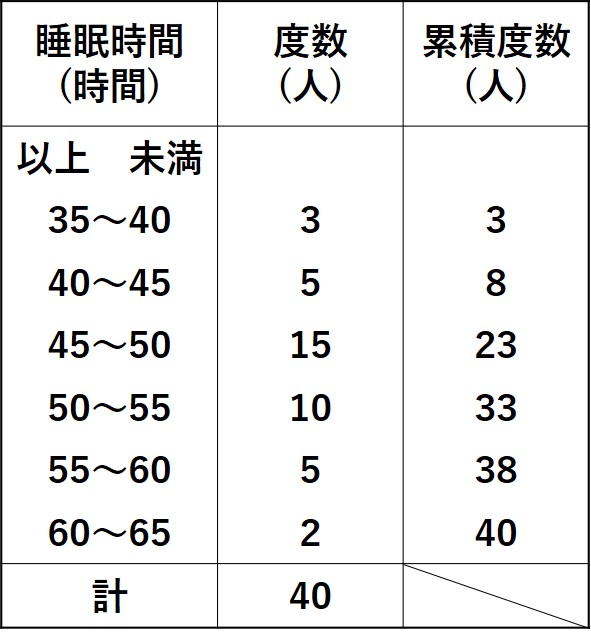
こちらを元に、「度数折れ線」を作成すると、このようになります。

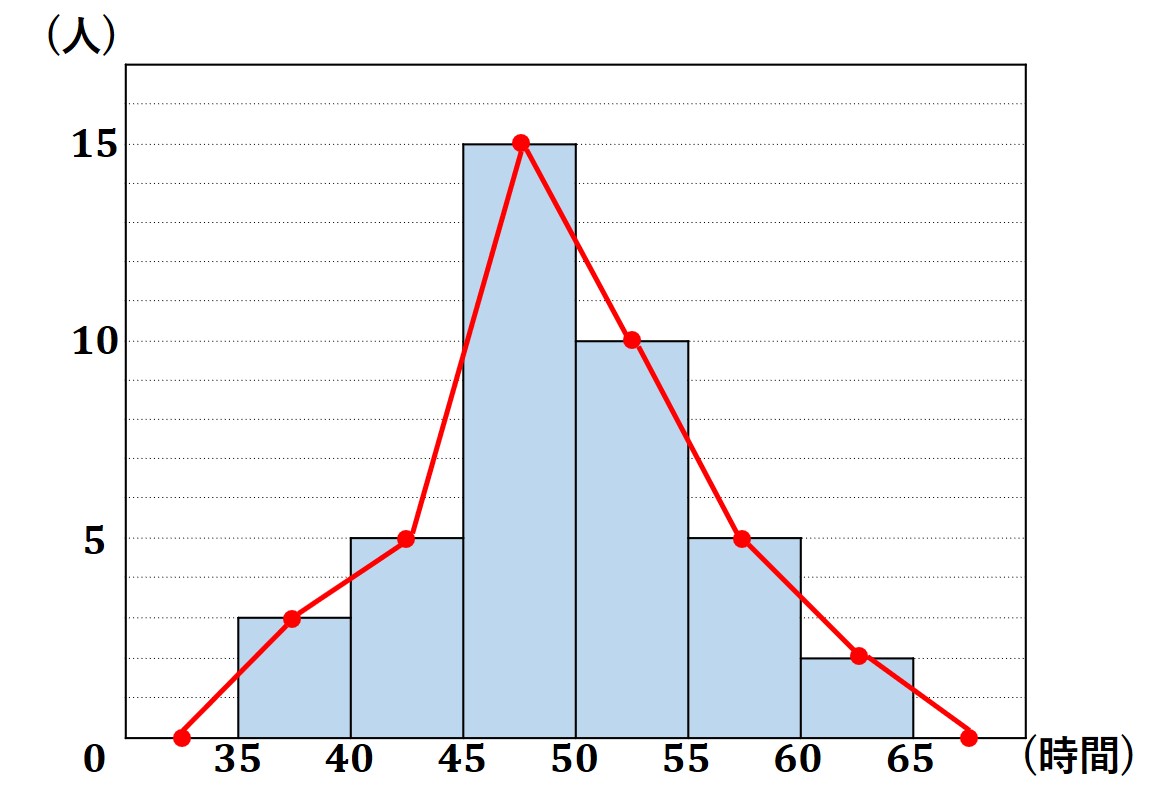
＜補足＞

２つのデータを比べたときに、平均値が同じになったとしても、範囲を調べることで、

・範囲が大きいほど、「データが散らばっている」
・範囲が小さいほど、「データが（平均付近に）集まっている」

と考えることができます。

＜まとめ＞

・データの中の「最大値と最小値の差」を範囲（レンジ）という
・「ヒストグラムの各長方形の上辺の中点を結んだグラフ」を度数折れ線という
・度数折れ線を書くとき、「左端は１つ前の階級の度数を0、右端は１つ先の階級の度数を0」とする