<ポイント>
・図形を「ある直線を折り目として、折り返した位置に移す」移動を対称移動という
・折り返したときに「両側の部分がぴったり重なる図形」を線対称な図形という
・対称の軸は「対応する2点を結ぶ線分」を垂直に2等分する直線になっている
図形を「ある直線を折り目として、折り返した位置に移す」移動を対称移動といいます。
このとき、「折り目となる直線」を対称の軸といいます。
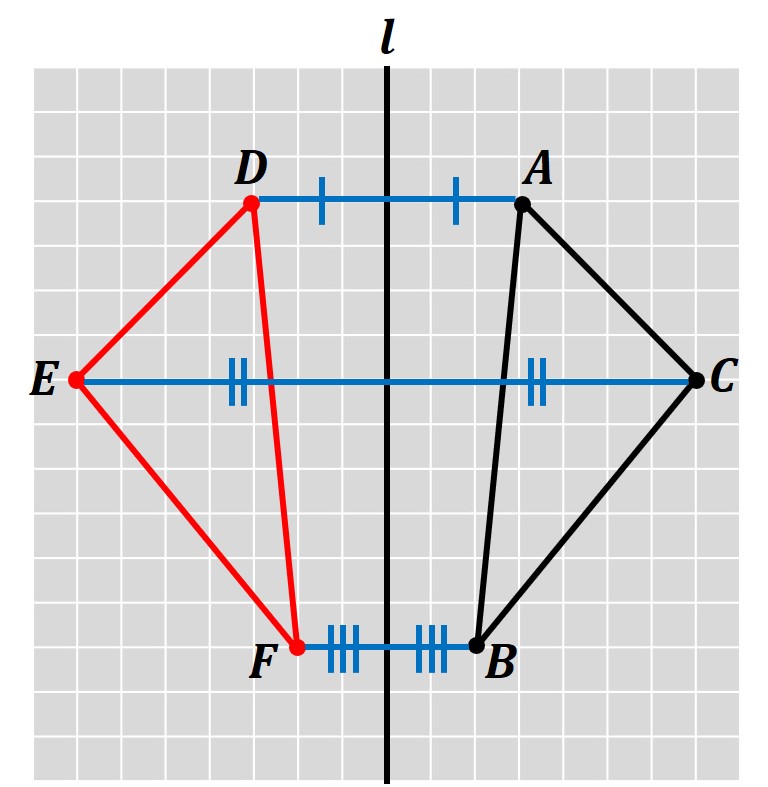
この図は「直線lを対称の軸とし、△ABCを対称移動させて△DEFをつくった」ことを表しています。
このとき、「折り目となる直線」を対称の軸といいます。

この図は「直線lを対称の軸とし、△ABCを対称移動させて△DEFをつくった」ことを表しています。
このとき、△ABCと△DEFは、直線lで折り返したとき、「両側の部分がぴったり重なる図形」です。
このような図形を、線対称な図形といいます。
また、対称の軸は「対応する2点を結ぶ線分」を垂直に2等分する直線になっています。
つまり、〔点Aから直線lまでの距離〕=〔点Dから直線lまでの距離〕となっているということです。
これは、他の対応する点においても言えることです。
<補足>
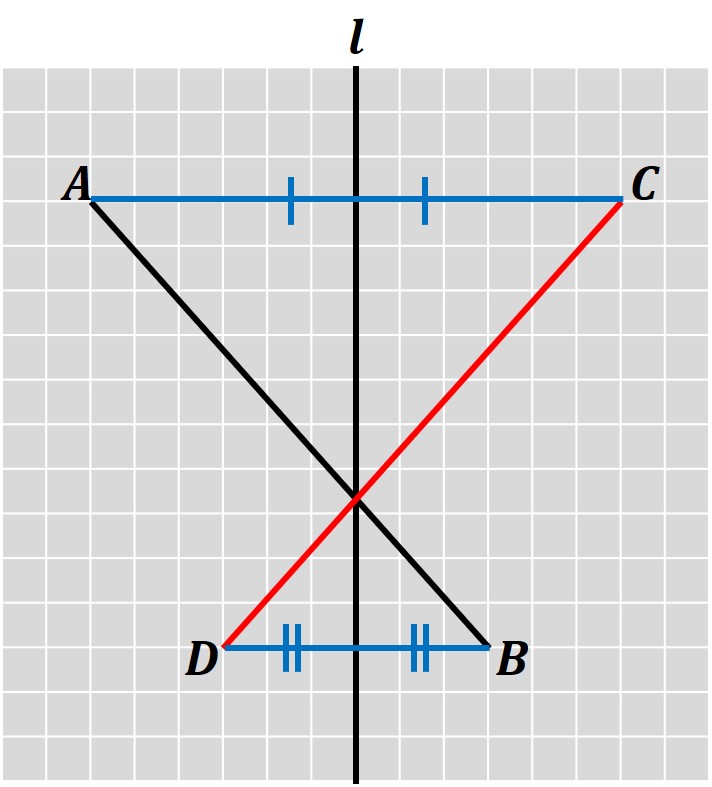
線対称な図形は、三角形や四角形などの多角形だけでなく、「直線(線分)でも表すことができる」ことを覚えておきましょう。
こちらの図は、線分ABを対称移動させ、線対称な線分CDを描いたものです。
<まとめ>
・図形を「ある直線を折り目として、折り返した位置に移す」移動を対称移動という
・折り返したときに「両側の部分がぴったり重なる図形」を線対称な図形という
・対称の軸は「対応する2点を結ぶ線分」を垂直に2等分する直線になっている
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

