図形を「ある点を中心として、一定の角度だけ回転させる移動」のことを回転移動といいます。

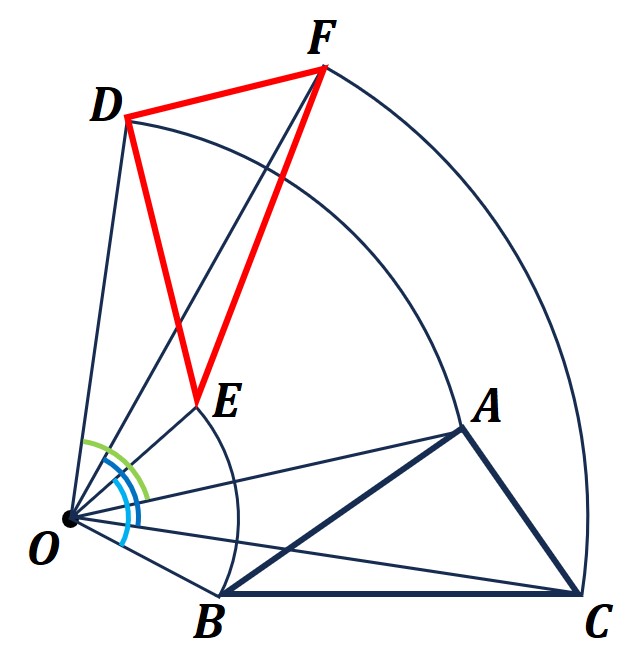
こちらの図は「△ABCを△DEFの位置まで、点Oを中心にして回転移動した」ことを示しています。
このとき、点Oのことを回転の中心といいます。

このとき、
・∠DOA（黄緑）＝∠EOB（水色）＝∠FOC（青色）
・DO＝AO, EO＝BO, FO＝CO
が成り立ちます。

回転移動した各点の軌跡は、「おうぎ形の弧を描く」ことになります。

また、点ではなく辺に注目すると、
辺ABが移動すると、辺DEになります。

このとき、AB＝DE となっています。
これは、他の辺についても同様のことがいえますし、当然、回転移動してできた図形は「回転させることでもとの図形と重ね合わせることができ」ます。

＜補足＞

図形を「180°だけ回転移動させること」を、点対称移動といいます。
点対称移動させた図形は、もとの図形と比べて上下左右が逆さまに描かれます。

＜まとめ＞

・図形を「ある点を中心として、一定の角度だけ回転させる移動」のことを回転移動という
・中心とする点を「回転の中心」という
・回転移動してできた図形は、回転させることでもとの図形と重ね合わせることができる