図形を「一定の方向に、一定の距離だけ移動させる」ことを平行移動といいます。
（図形をそのまま「スライドさせる」イメージ）

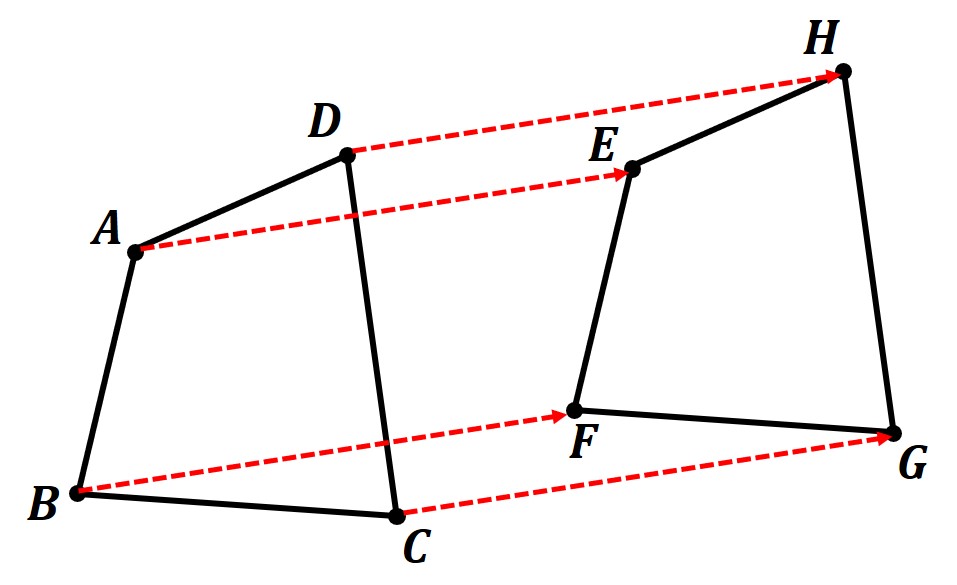
こちらの図は「四角形ABCDを四角形EFGHの位置まで平行移動した」ことを示しています。

このとき、
・AE//BF//CG//DH
・AE＝BF＝CG＝DH
が成り立ちます。

平行移動した各点の軌跡は、「平行かつ等しい」ということです。
（軌跡とは、各点が移動した様子を示した線分のこと）

また、点ではなく辺に注目すると、
辺ADが移動すると、辺EHになります。

このとき、AD//EH かつ AD＝EH となっています。

これは、他の辺についても同様のことがいえます。

＜補足＞

図形の移動の前後において、「移動前の点」と「移動後の点」を対応する点、
「移動前の辺」と「移動後の点」を対応する辺といいます。

＜まとめ＞

・「形や大きさを変えずに」図形を他の位置に移すことを図形の移動という
・図形を「一定の方向に、一定の距離だけ移動させる」ことを平行移動という
・平行移動した各点の軌跡は、「平行かつ等しい」