〔例題〕
y＝(2/3)x　（－3≦x≦6）のグラフを描きなさい。

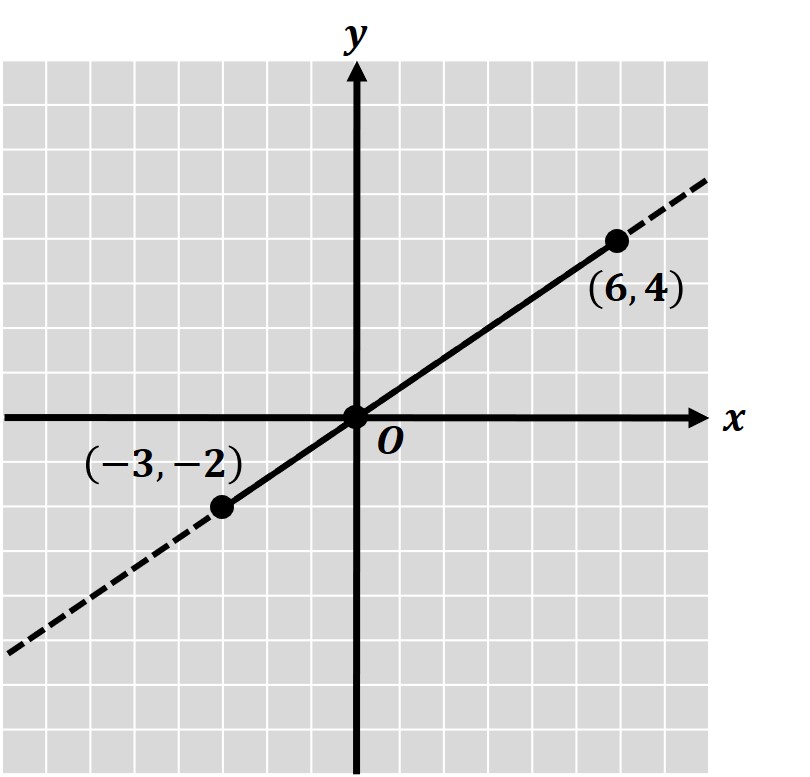
こちらのグラフを描く手順はこのようになります。

①変域のあるグラフは、まず変域を気にせずにグラフを描く
　
　この場合は、y＝(2/3)x のグラフを描きます。
（原点から「右に3, 上に2 進んだところにある（3, 2）」と原点を結んで伸ばす）

②変域の外になる部分については、点線に変える

今回の場合、xの変域は－3≦x≦6 なので、
「x＝－3より左側」「x＝6より右側」の部分を一旦消して、
そのあと「点線で、あらためて描く」とグラフをつくれます。

③端の数を含む場合は●を使って表し、含まない場合は◯を使って表す

また、変域を表す不等号が「＜」か「≦」の「＝の有無」によって、グラフの端の部分が決まります。

「≦」の場合は「グラフの端の数を含む」ので、●で表します。
「＜」の場合は「グラフの端の数を含まない」ので、〇で表します。

今回の場合、（－3≦x≦6）で「両方とも＝がある」ため、グラフの両端が●になっています。

＜補足＞

xの変化できる範囲を変域といいますが、それに対する「yの変化する範囲」を値域といいます。

このグラフの場合、値域は －2≦y≦4 となります。

＜まとめ＞

・変域のあるグラフは、まず変域を気にせずにグラフを描く
・変域の外になる部分については、点線に変える
・端の数を含む場合は●を使って表し、含まない場合は◯を使って表す