（１）グラフから比例の式を求める（代入）
グラフの通っている点の座標を読み取り、y＝ax に代入すると比例定数を求めることができます。

〔例題〕
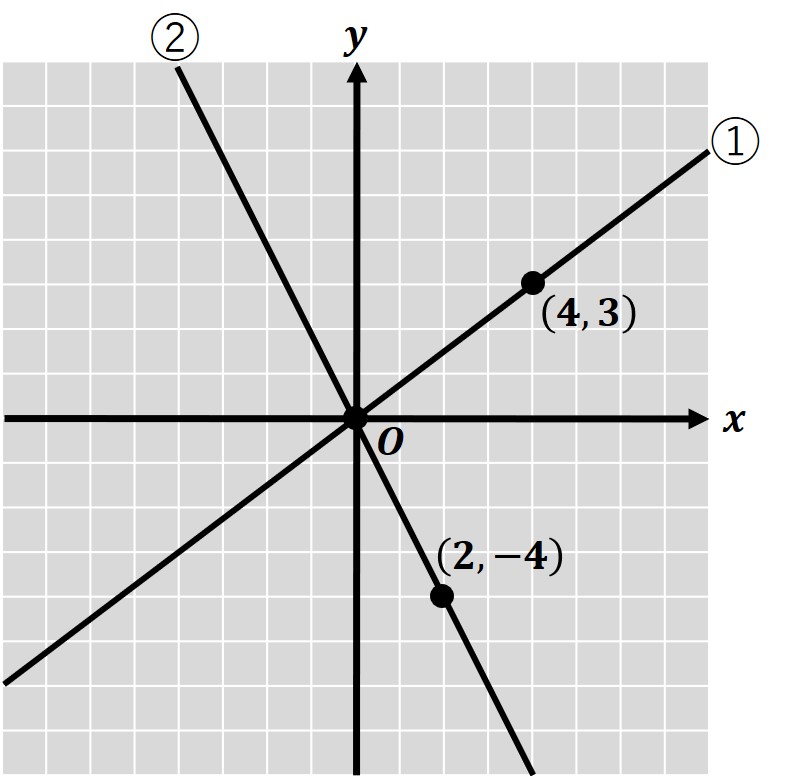
下の比例のグラフで表される、①と②の式を求めなさい。

①は点（4, 3）を通っているので、y＝ax に代入します。

x＝4, y＝3を代入すると、
4a＝3
a＝3/4
したがって、y＝(3/4)x
 
 
②は点（2, －4）を通っているので、y＝ax に代入します。

x＝2, y＝－4を代入すると、
2a＝－4
a＝－2
したがって、y＝－2x

（２）グラフから比例の式を求める（変化の仕方）
次は、原点から見て、「xが増加したとき、yがどのように変化するのか」を読み取ることで式を求めてみます。

これは、y＝ax の a（比例定数）は [yの変化量] / [xの変化量] で求めることができ、その値が一定であることを利用します。

（上のグラフの）
①は、原点から点（4, 3）を見ると、
x が 4 増加したときに、y が 3 増加しています。
（原点から（4, 3）まで、右に 4 進み、上に 3 進んでいる）

このことから、
[yの変化量] / [xの変化量] ＝ 3/4
つまり、a＝3/4 なので、y＝(3/4)x

同様に、
②は、原点から点（2, －4）を見ると、
x が 2 増加したときに、y が 4 減少しています。
（原点から（2, －4）まで、右に 2 進み、上に －4 進んでいる）

このことから、
[yの変化量] / [xの変化量] ＝ －4/2 ＝－2
つまり、a＝－2 なので、y＝－2x

＜補足＞

グラフが右下がりになっているとき、a＜0 となります。
「右下がり」＝右に進むと、下に下がる

つまり、「xが増加すると、yが減少していく」ということです。
このことを、a＝[yの変化量] / [xの変化量]
に当てはめると、「aが負になる」ことが分かります。

＜まとめ＞

・グラフの通っている点の座標を読み取り、y＝ax に代入する
・原点から見て、「xが増加したとき、yがどのように変化するのか」を読み取る
・y＝ax の a（比例定数）は [yの変化量] / [xの変化量] で求めることができる