これは、以下のことから言えることです。

・x＝0 のとき、必ず y＝0 となるため（原点を通る）
・「x を2倍, 3倍…とすると、y も2倍, 3倍…となる」ことから一定の割合で変化すると言える（グラフが直線になる）
 
 
（2）グラフの向き
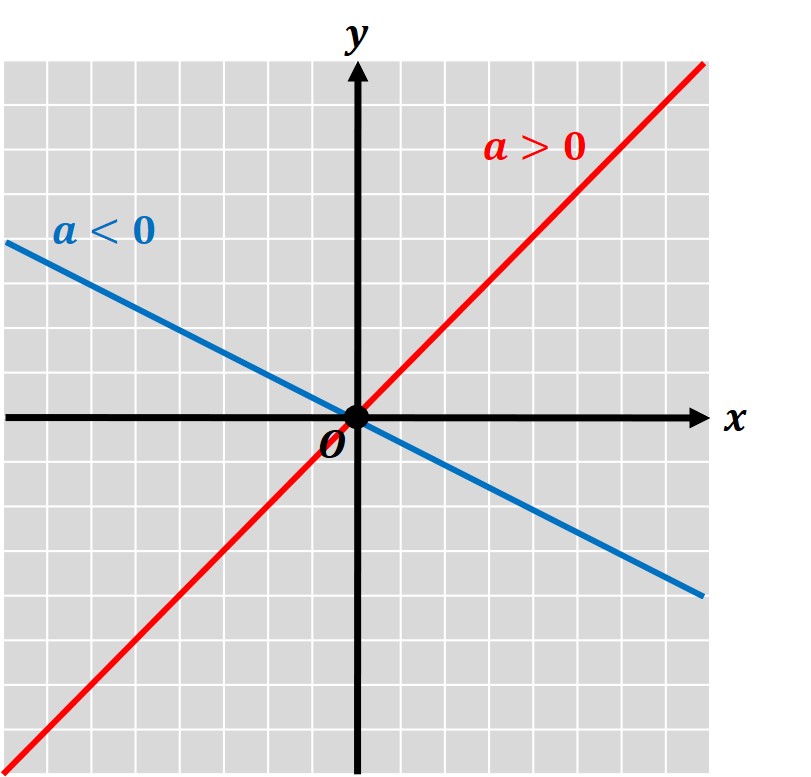
グラフが「どのような向きで描かれるか」は、a の符号によって決まります。
y＝ax の「a＞0 のとき、グラフは右上がり」（a が正の値）となり、
「a＜0 のとき、グラフは右下がり」（a が負の値）となります。

（３）比例のグラフの描き方
比例のグラフは、「必ず原点を通り、直線で描かれる」ため、原点以外のグラフが通る点を見つけると描けます。
なぜなら、「２点を結べば、直線が描けるから」です。

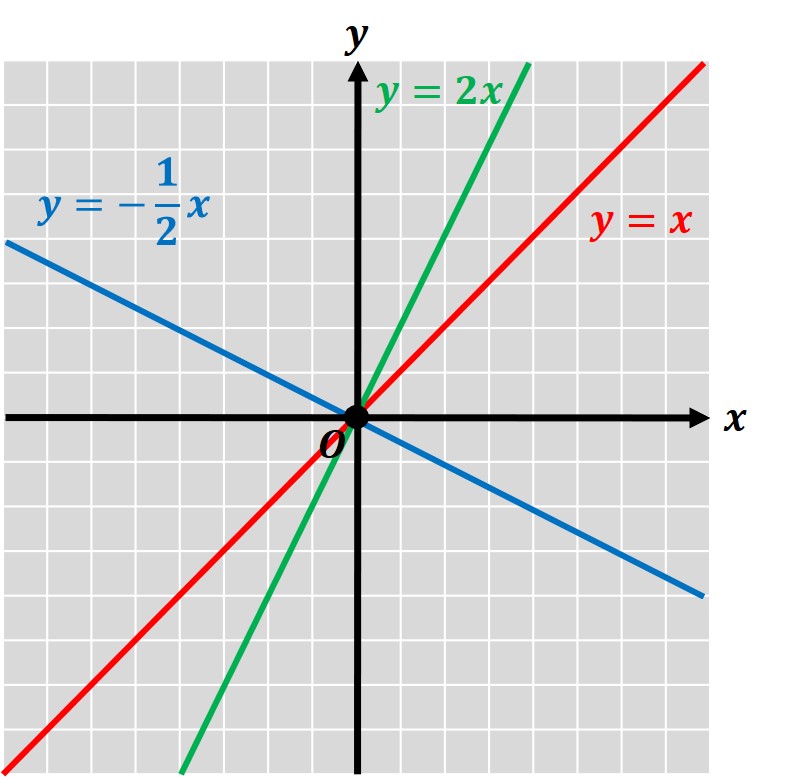
〔赤いグラフ〕
y＝x のグラフを描きたい場合、
x＝1 のとき、y＝1 となるため、点（1, 1）を通ります。
原点と（1, 1）を結んでできる直線が、y＝x のグラフということです。

〔緑のグラフ〕
y＝2x のグラフを描きたい場合、
x＝1 のとき、y＝2 となるため、点（1, 2）を通ります。
原点と（1, 2）を結んでできる直線が、y＝2x のグラフということです。

〔青いグラフ〕
y＝－(1/2)x のグラフを描きたい場合、
x＝2 のとき、y＝－1 となるため、点（2, －1）を通ります。
原点と（2, －1）を結んでできる直線が、y＝－(1/2)x のグラフということです。

＜補足＞

上の〔青いグラフ〕を描くとき、他のものは x＝1 のときを考えたのに、x＝2のときを考えました。
これは、「y座標が整数となるように、あえて x＝2 を代入した」のです。

グラフを描くときは、「x座標、y座標がともに整数となるような点」を使って考えるようにしましょう。

＜まとめ＞

・
・
・・比例 y＝ax のグラフは原点を通る直線になる
・y＝ax の「a＞0 のとき、グラフは右上がり」、「a＜0 のとき、グラフは右下がり」
・原点以外の「グラフが通るもう1点を見つける」（2点を結ぶと直線は描ける）