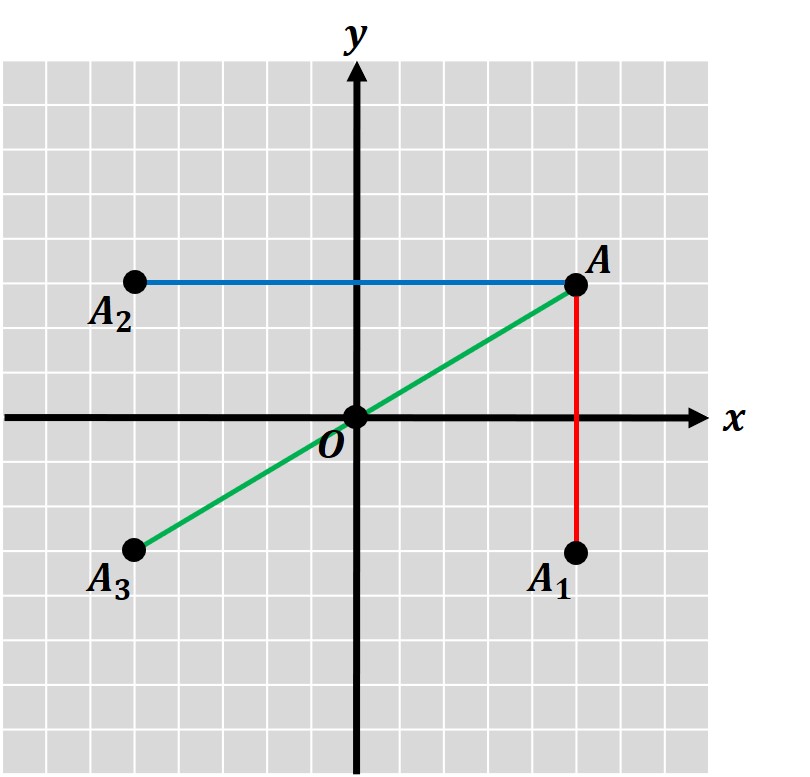
（１）x軸について対称な点
点Aと「x軸について」対称な点A₁は、x軸を折り目として折るときに重なる点です。
このようにして折ると、x座標は変わらず、y座標の符号が逆になることが分かります。

このことから、A（5, 3）なので、
点Aと「x軸について」対称な点A₁の座標は、A₁（5, －3）となります。
 
 
（２）y軸について対称な点
点Aと「y軸について」対称な点A₂は、y軸を折り目として折るときに重なる点です。
このようにして折ると、y座標は変わらず、x座標の符号が逆になることが分かります。

このことから、A（5, 3）なので、
点Aと「y軸について」対称な点A₂の座標は、A₂（－5, 3）となります。
 
 
（３）原点について対称な点
点Aと「原点について」対称な点A₃は、原点を中心として180°回転させたときに重なる点です。
このようにして回転させると、x座標、y座標ともに符号が逆になることが分かります。

このことから、A（5, 3）なので、
点Aと「原点について」対称な点A₃の座標は、A₃（－5, －3）となります。
 
 
（４）点の移動
座標平面上で、「点を移動させる」ことがあります。

「x軸に沿って、右へ〇・左へ●」などと表現され、
「右へ移動する」場合は＋の方へ移動するため、x座標は大きくなります。
反対に、「左へ移動する」場合は－の方へ移動するため、x座標は小さくなります。

同様に、y軸の場合は「y軸に沿って、上へ〇・下へ●」などと表現され、
「上へ移動する」場合は＋の方へ移動するため、y座標は大きくなります。
反対に、「下へ移動する」場合は－の方へ移動するため、y座標は小さくなります。

〔例題〕
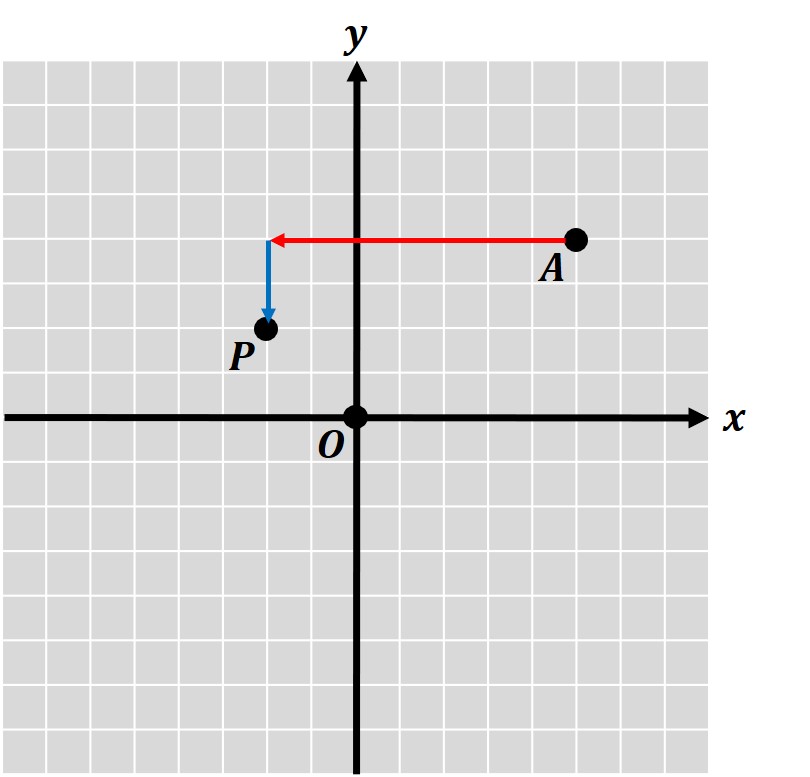
点A（5, 4）を、x軸に沿って左へ7、y軸に沿って下へ2 移動させたときの点Pの座標を求めなさい。

「x軸に沿って左へ7」移動すると、－方向への移動のため x座標が 7 小さくなり、
「y軸に沿って下へ2」移動すると、－方向への移動のため y座標が 2 小さくなります。

したがって、点Aの座標を参考にして点Pの座標を求めると、

点P（5－7, 4－2）
⇒点P（－2, 2）となります。

＜補足＞

点の移動について、「x軸方向へ〇移動する」や「y軸方向に●移動する」などと表現されることがあります。

「x軸方向へ〇移動する」というのは、x軸の矢印が向いている方向つまり「xの正の方向へ移動する」ことを意味しています。
同様に、「y軸方向へ●移動する」というものは、「yの正の方向へ移動する」と考えてください。

＜まとめ＞

・x軸について対称⇒ y座標の符号だけが変わる
・y軸について対称⇒ x座標の符号だけが変わる
・原点について対称⇒ x座標、y座標の両方の符号が変わる