（1）関数
「xの値を決めると、それに対応するyの値が1つに決まる」もの（式）を関数といいます。

たとえば、

「時速5kmで x 時間歩いたときの道のり y km」
という関係を文字を使った式で表すと、y＝5x となります。
（〔道のり〕＝〔速さ〕×〔時間〕で求められる）

具体的な値をxに代入して、yを求めてみると、
x＝1 とすると、y＝5・1＝5
x＝2 とすると、y＝5・2＝10
のようになり、「xの値を決めると、それに対応するyの値が1つに決まる」ことになります。

よって、y＝5x という式において、「y は x の関数である」といえます。
 
 
（2）変数と変域
（決められた範囲の中で）どんな値でもとることができる文字を変数といい、
「変数のとりうる値の範囲」を変域といいます。

この変域を表すときには、「不等号を使った式（不等式）」で表します。

〔例題〕
変数 x が次のような範囲を表すとき、その変域を不等号を使って表しなさい。

① −5 以上で 2 より小さい
「〜以上・以下」の表現はその数を含むため、等号（＝）がつきます。
「〜より小さい・大きい」の表現は、その数を含みません。
したがって、−5 ≦ x ＜ 2

② 12未満の数
「〜未満」は、その数を含まない表現です。
（「〜未満」と「〜より小さい」は同じ意味）
したがって、x ＜ 12

＜補足＞

変域を数直線上に表すとき、以下のような決まりがあります。

その端の数を含む場合は●を使って表し、含まない場合は◯を使って表します。

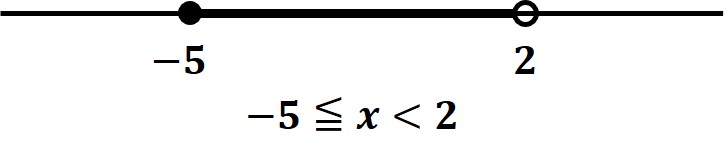
たとえば、−5 ≦ x ＜ 2 を数直線に表すと、このようになります。

＜まとめ＞

・関数とは、「xの値を決めると、それに対応するyの値が1つに決まる」もの
・（決められた範囲の中で）どんな値でもとることができる文字を変数という
・「変数のとりうる値の範囲」を変域という