<ポイント>
・おうぎ形は「円の一部」というイメージ
・弧 l =2πr・(x/360)
・面積 S =πr2・(x/360)
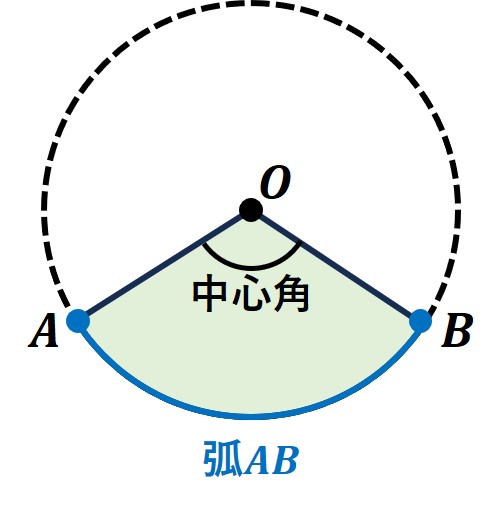
(1)おうぎ形
おうぎ形は「円の一部を切り取ったもの」です。
このようにイメージしておくと、「弧の長さ」「面積」ともに、円一つ分のものを求めたものに「おうぎ形が占める割合」をかけてあげることが分かります。
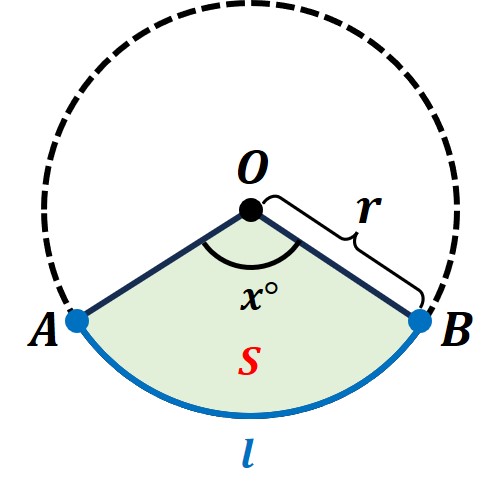
(2)弧の長さ
〔弧の長さ〕=〔円周の長さ〕×〔おうぎ形の割合〕より、
半径=r のとき、
〔弧の長さ〕=2πr・(x/360)
で求めることができます。
(3)おうぎ形の面積
〔おうぎ形の面積〕=〔円の面積〕×〔おうぎ形の割合〕より、
半径=r のとき、
〔おうぎ形の面積〕=πr2・(x/360)
で求めることができます。
【練習】
① 半径8cm、中心角45°のおうぎ形の弧の長さは?
〔弧の長さ〕=2πr・(x/360)
=16π・(1/8)=2π cm
おうぎ形は「円の一部を切り取ったもの」です。
このようにイメージしておくと、「弧の長さ」「面積」ともに、円一つ分のものを求めたものに「おうぎ形が占める割合」をかけてあげることが分かります。

(2)弧の長さ
〔弧の長さ〕=〔円周の長さ〕×〔おうぎ形の割合〕より、
半径=r のとき、
〔弧の長さ〕=2πr・(x/360)
で求めることができます。
(3)おうぎ形の面積
〔おうぎ形の面積〕=〔円の面積〕×〔おうぎ形の割合〕より、
半径=r のとき、
〔おうぎ形の面積〕=πr2・(x/360)
で求めることができます。

【練習】
① 半径8cm、中心角45°のおうぎ形の弧の長さは?
〔弧の長さ〕=2πr・(x/360)
=16π・(1/8)=2π cm
② 半径12cm、中心角120°のおうぎ形の面積は?
〔おうぎ形の面積〕=πr2・(x/360)
=144π・(1/3)=48π cm2
<補足>
おうぎ形の「中心角の大きさ」と「弧の長さ」は比例します。
このことから、
〔円周の長さ〕:〔弧の長さ〕=〔一周分 360°〕:〔中心角 x°〕
という関係が成り立ちます。
そのため、「半径と弧の長さがそれぞれ分かっている」場合には、中心角 x°の大きさを求めることができます。
〔例〕半径8cmで、弧の長さが10π cmであるおうぎ形の中心角の大きさは何度か?
〔円周の長さ〕:〔弧の長さ〕=〔一周分 360°〕:〔中心角 x°〕
16π:10π=360:x
16πx=3600π
x=225°
<まとめ>
・おうぎ形は「円の一部」というイメージ
・弧 l =2πr・(x/360)
・面積 S =πr2・(x/360)
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

