<ポイント>
・円周上に2点A,Bをとるとき、「点AからBまでの円周の一部分」を弧ABという
・「弧ABの両端を結んだ線分」を弦ABという
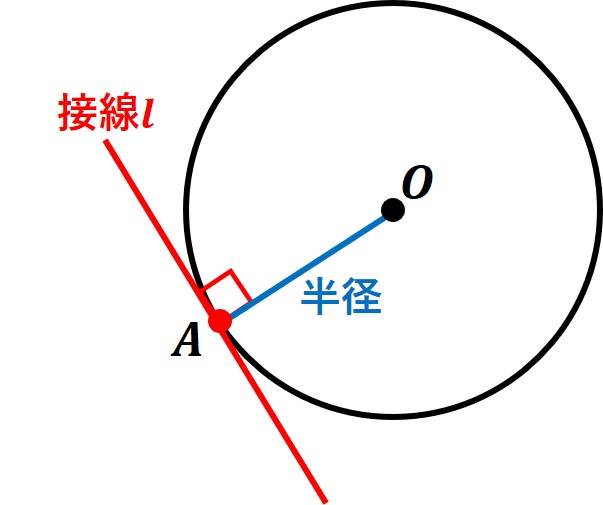
・円の接線は、その接点を通る半径に垂直になる
(1)弧
円周上に2点A,Bをとるとき、「点AからBまでの円周の一部分」を弧ABといいます。
(弧ABは(円周上に)ふつう2つ存在しますが、どちらであるかを区別するために、その途中の点Cなどを用いることがあります)
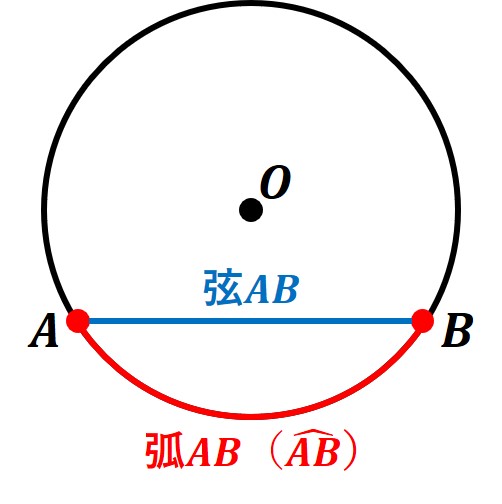
弧ABは記号を使うと、以下のように表します。

この場合は「円周上の点〇と●の間の部分」を表していて、その通る点の上に「丸かっこ」をかぶせるような記号を使います。
(2)弦
「弧ABの両端を結んだ線分」を弦ABといいます。
(弓やギターの弦をイメージすると、直線であることがわかる)
円にできる弦の中で「最も長いもの」は、その円の直径になります。
また、弦は「半径と直角に交わる」という性質があります。
(3)円の接線
円Oが、直線lと1点だけを共有する位置関係を「接する」といいます。
このとき、円に接する直線を接線、共有する点を接点といいます。
円周上に2点A,Bをとるとき、「点AからBまでの円周の一部分」を弧ABといいます。
(弧ABは(円周上に)ふつう2つ存在しますが、どちらであるかを区別するために、その途中の点Cなどを用いることがあります)

弧ABは記号を使うと、以下のように表します。

この場合は「円周上の点〇と●の間の部分」を表していて、その通る点の上に「丸かっこ」をかぶせるような記号を使います。
(2)弦
「弧ABの両端を結んだ線分」を弦ABといいます。
(弓やギターの弦をイメージすると、直線であることがわかる)
円にできる弦の中で「最も長いもの」は、その円の直径になります。
また、弦は「半径と直角に交わる」という性質があります。
(3)円の接線
円Oが、直線lと1点だけを共有する位置関係を「接する」といいます。
このとき、円に接する直線を接線、共有する点を接点といいます。
円の接線は「その接点を通る半径に垂直になる」という性質があります。
<補足>
円の接線を作図する場合は、(上の図の)
半径OAを延長して「接点Aを通る垂線」をつくります。
(「接線と半径は垂直に交わる」ため)
<まとめ>
・円周上に2点A,Bをとるとき、「点AからBまでの円周の一部分」を弧ABという
・「弧ABの両端を結んだ線分」を弦ABという
・円の接線は、その接点を通る半径に垂直になる
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

