| 〔質問〕 ひし形の内接円の中心は、ひし形の対角線の交点になるらしいですが、なぜでしょうか? |
| 〔回答〕 「内接」というのは、すべての辺と円が接することを意味しますので、 少なくとも、ひし形の向かい合う2辺(平行の2辺)については、円とはこういう関係のはずで、 この円の中心は「ちょうど真ん中の平行線(緑線)」上にあるはずです。 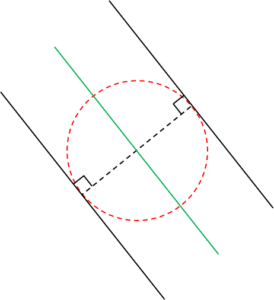 (※ もちろん円の中心は黒の点線の中点ですが、ひし形の内接円を考えるに当たってはそもそも接点の場所が不明なため、「真ん中の平行線」というような考え方をしています) これはもう1組の2辺の方でも言えますので、よって、それらの交点が内接円の中心ということになり、 かつ、この点は(分割されてできた4つの小さいひし形が合同であることから)元のひし形の対角線の中点(=対角線の交点)になっています。  |
〔補足〕
四角形の場合、必ずしも内接円が存在するとは限りません(三角形の場合は必ず存在)。
ですので、証明の際、本来は「ひし形の場合は内接円が存在する」ことも含めて示す必要があります(内接円が存在することを前提に話を進めてはいけない)。
四角形の場合、必ずしも内接円が存在するとは限りません(三角形の場合は必ず存在)。
ですので、証明の際、本来は「ひし形の場合は内接円が存在する」ことも含めて示す必要があります(内接円が存在することを前提に話を進めてはいけない)。
上記の説明の場合、(内接円が存在しないはずの)一般的な平行四辺形についても言える話になっており、まだ「内接円が存在しているのなら、この点以外にはありえない」ということを言ったにすぎません。
これに加えて、「ひし形の場合は、この交点から各辺までの垂線の長さが等しい」ということを言えば、内接円が存在していることも含めて示せていることになります。
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

