| 〔質問〕 辺の長さがすべて分かっている正三角錐の、高さの求め方ってありますか? |
| 〔回答〕 △BCDが正三角形、点MはCDの中点とします。 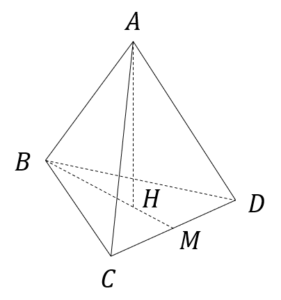 点Aから△BCDに垂線を下ろして、その足を点Hとおくと、正三角錐(正四面体も含む)の場合は「点Hは△BCDの重心」になり、 以上を踏まえて、 |
〔詳細〕
「点Hは△BCDの重心になる」理由ですが、
まず、△ABH、△ACH、△ADH を見てもらうと、
・それぞれHの所で直角の直角三角形、
・AB=AC=AD
・AH 共通
ですので合同ということになり、
よって、BH=CH=DH が得られます。

ということは、底面の方で、△BCH≡△CDH≡△DBH(かつ、それぞれ二等辺三角形)となりますので、例えば ∠BCH=∠DCH=30° というのが得られます。
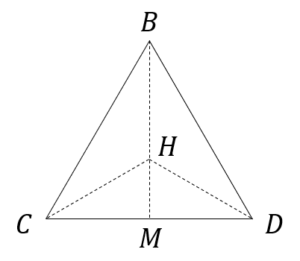
△CHMは直角三角形(かつ ∠MCH=30°)ですので、よって、CH:HM=2:1 が得られ、かつ CH=BH より、BH:HM=2:1 ということになります。
「点Hは△BCDの重心になる」理由ですが、
まず、△ABH、△ACH、△ADH を見てもらうと、
・それぞれHの所で直角の直角三角形、
・AB=AC=AD
・AH 共通
ですので合同ということになり、
よって、BH=CH=DH が得られます。

ということは、底面の方で、△BCH≡△CDH≡△DBH(かつ、それぞれ二等辺三角形)となりますので、例えば ∠BCH=∠DCH=30° というのが得られます。

△CHMは直角三角形(かつ ∠MCH=30°)ですので、よって、CH:HM=2:1 が得られ、かつ CH=BH より、BH:HM=2:1 ということになります。
(正確には、∠CBH=30° より、(∠CBH=∠CBM ということで)B, H, M が一直線上にある、も言う必要がある)
※ 重心自体の説明についてはこちらを参照してください
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

