<ポイント>
・回路を流れる電流は「川を流れる水」とイメージする
・直列回路を流れる電流の大きさは、どこでも同じ大きさ
・並列回路を流れる電流の大きさは、「分かれる前=合流後」という関係になる
・回路を流れる電流は「川を流れる水」とイメージする
・直列回路を流れる電流の大きさは、どこでも同じ大きさ
・並列回路を流れる電流の大きさは、「分かれる前=合流後」という関係になる
「回路を流れる電流」は、「川を流れる水」とイメージすると分かりやすいです。
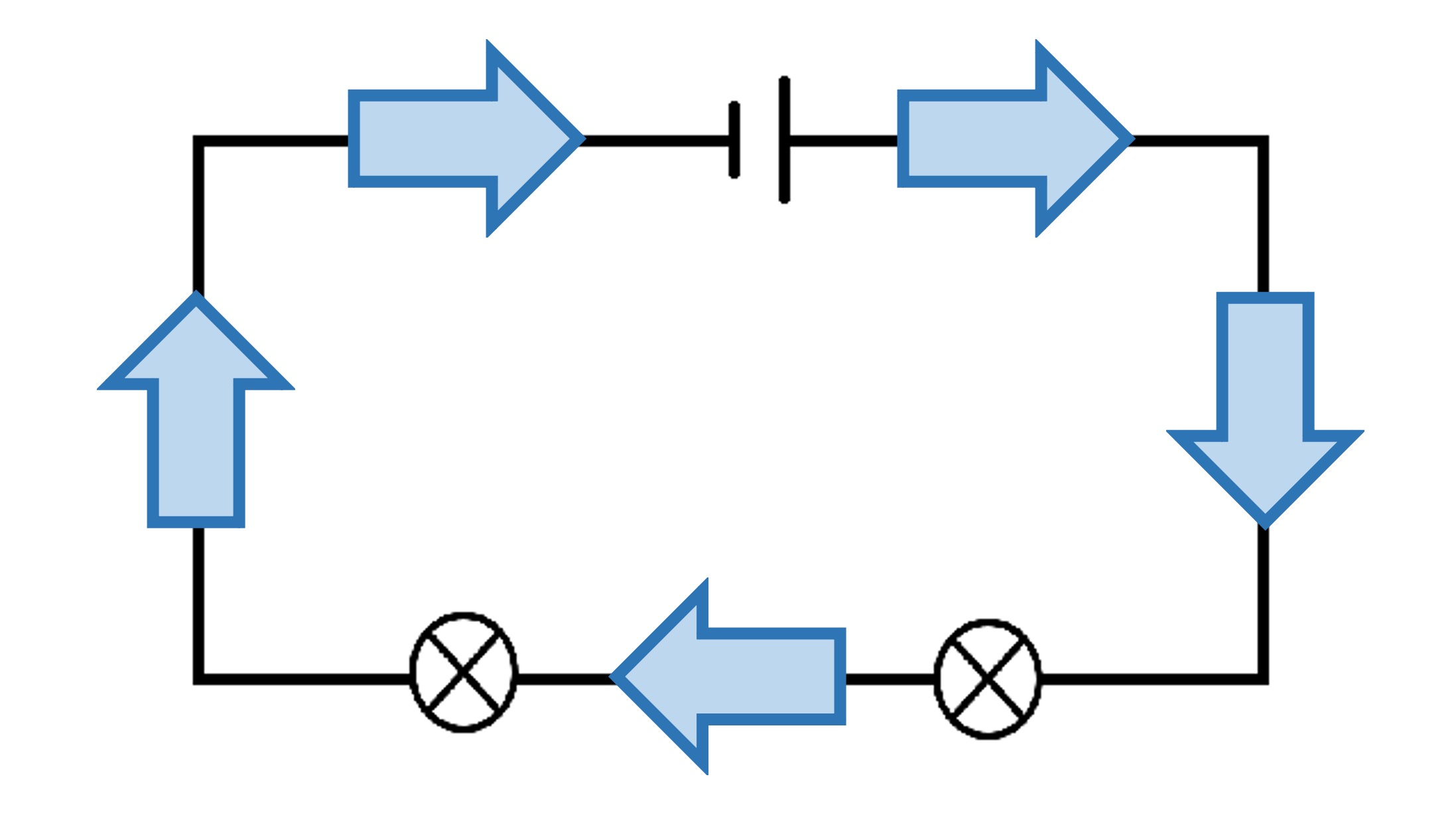
水が流れるときは、1本道(直列)の場合はどこでも同じ量が流れていて、枝分かれ・合流がある(並列)の場合も「分かれる前後で同じ量」が流れます。

水が流れるときは、1本道(直列)の場合はどこでも同じ量が流れていて、枝分かれ・合流がある(並列)の場合も「分かれる前後で同じ量」が流れます。
このことをイメージしながら、直列回路・並列回路を流れる電流の大きさについて見ていきます。
(1)直列回路を流れる電流
.jpg)
直列回路は1本道のため、どこでも流れる量は同じと考えられます。
したがって、IA=IB=ICという関係になっています。
(2)並列回路を流れる電流
.jpg)
並列回路は、途中で「枝分かれしたあと、合流する」ような回路です。
「分かれる前後で同じ量」が流れていると考えられます。
したがって、IA=IB+IC=IDとなります。
ただ注意が必要なのは、「IB=ICとなるかは不明」ということです。
枝分かれした部分にある抵抗の大きさが違う場合は、それぞれの経路に流れる電流の大きさは異なります。
(抵抗の大きさが同じであれば、同じ大きさの電流が流れる)
ただひとつ言えることは、「枝分かれしている部分に流れる電流の和は、枝分かれする前後の電流の大きさに等しい」ということです。
<補足>
当たり前のことのようで、勘違いしやすいのが、「豆電球を通ったあとの電流の大きさの方が小さい?」ということです。
「豆電球を光らせるために電流が使われるのでは??」と考えてしまいますが、これは間違いです。
豆電球などの抵抗を通る前後では、流れる電流の大きさは等しくなっています。注意しましょう。
当たり前のことのようで、勘違いしやすいのが、「豆電球を通ったあとの電流の大きさの方が小さい?」ということです。
「豆電球を光らせるために電流が使われるのでは??」と考えてしまいますが、これは間違いです。
豆電球などの抵抗を通る前後では、流れる電流の大きさは等しくなっています。注意しましょう。
<まとめ>
・回路を流れる電流は「川を流れる水」とイメージする
・直列回路を流れる電流の大きさは、どこでも同じ大きさ
・並列回路を流れる電流の大きさは、「分かれる前=合流後」という関係になる
・回路を流れる電流は「川を流れる水」とイメージする
・直列回路を流れる電流の大きさは、どこでも同じ大きさ
・並列回路を流れる電流の大きさは、「分かれる前=合流後」という関係になる
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|

