| 〔質問〕 三角形ABCの重心をOとした時に、OA+OB+OC=0となるのは正三角形の場合に成り立つのですか? また、外心をOとした時に上の式が成り立つのはどのような場合ですか? |
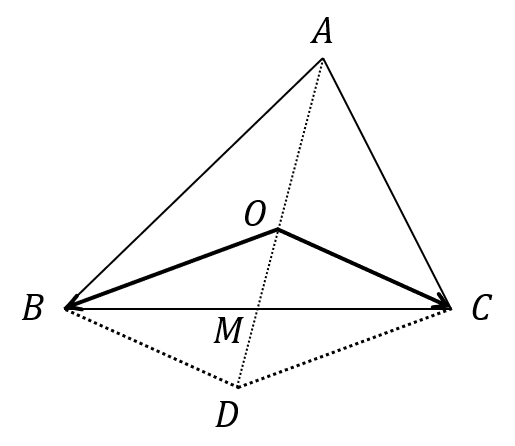
| 〔回答〕 ※ ベクトルの問題として回答します OA+OB+OC=0 ということは(どれでも構いませんが)移項すると OB+OC=-OA ということになりますが、 つまり、この図のような位置関係にあるということです。 このとき、平行四辺形の性質から、点Mは、 |
〔補足〕
なお、重心の件を式で端的に示すなら、OA+OB+OC=0 の両辺を 3 で割ると、(OA+OB+OC)/3=0 となりますが、
左辺が重心の位置ベクトルを表していて、それが右辺のゼロベクトルに等しいということは、「重心=始点」ということになります。
(正三角形がどうこうということに関係なく成り立っている)
なお、重心の件を式で端的に示すなら、OA+OB+OC=0 の両辺を 3 で割ると、(OA+OB+OC)/3=0 となりますが、
左辺が重心の位置ベクトルを表していて、それが右辺のゼロベクトルに等しいということは、「重心=始点」ということになります。
(正三角形がどうこうということに関係なく成り立っている)
| ※ 理解を優先するために、あえて大雑把に書いてある場合があります |
|---|
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |