（例題）2x²＋3xy－2y²＋11x＋7y＋15

（１）まず原則として、
・「x についての何次式か」「y についての何次式か」をチェックし（判断方法はこちら）、
・「次数が低い方の文字で整理する」
という手順をとる。
※ 次数の高い文字で整理しても因数分解自体は可能だが、低い文字で整理した方が計算が楽。

今回は、「x についての２次式」「y についての２次式」であるため、その場合はどちらで整理しても構わない。
 
 
（２）仮に x について整理すると、
2x²＋3xy－2y²＋11x＋7y＋15
＝2x²＋(3y＋11)x－2y²＋7y＋15（…①）となる。

先に －2y²＋7y＋15 の部分を因数分解すると（２次の係数・定数項で因数分解できる部分はしておく）、
①＝2x²＋(3y＋11)x－(2y²－7y－15)　
   ＝2x²＋(3y＋11)x－(y－5)(2y＋3) となる。
 
 
（３）ここから先は、2y²－7y－15 を (y－5)(2y＋3) に因数分解したのと同じ要領で行う。

2y²－7y－15 を因数分解する際、
・かけたら 2 になるもの（２次の係数）
・かけたら －15 になるもの（定数項）
のパターンを考え、
それをたすき掛けによって「－7」が得られる組合せを考えるが、

2x²＋(3y＋11)x－(y－5)(2y＋3) についても同様で、
・かけたら 2 になるもの
・かけたら －(y－5)(2y＋3) になるもの
のパターンを考え、
それをたすき掛けによって「(3y＋11)」が得られる組合せを考える。

試行錯誤しながら、

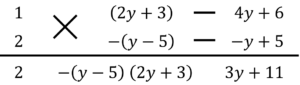
というのを見つけたら、
(x＋2y＋3){x－(y－5)} という当てはめ方をして、
最終的に整理した (x＋2y＋3)(x－y＋5) が答えとなる。

＜補足＞
途中で「２次の係数・定数項で因数分解できる部分はしておく」として、定数項部分を因数分解しておいたのは、
その後で、
・かけたら 2 になるもの
・かけたら －(y－5)(2y＋3) になるもの
のパターンを考える必要があることを見越してのもの。

＜まとめ＞
・x の項や定数項が文字式であっても、数字のときと同じようにたすき掛けしていく