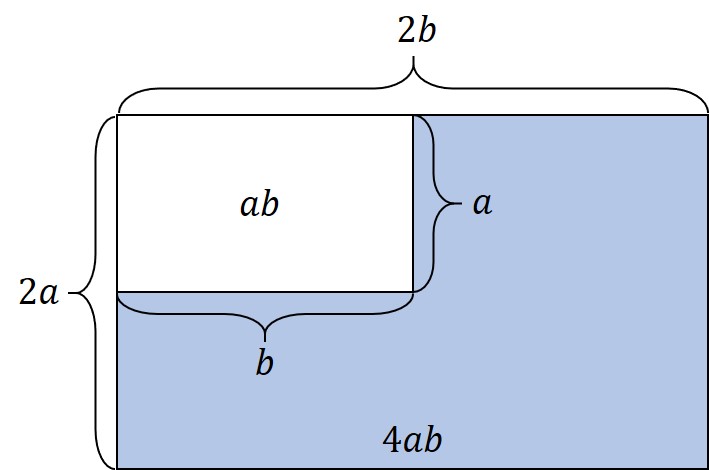
たとえば、実際の大きさが0.1mmの物体のとき、倍率が10倍のレンズで見れば（レンズ越しでは）1.0mmの大きさに拡大されて見え、同じ物体を20倍の倍率で観察すれば2.0mmで見えていることになります。
このように「倍率自体が2倍になると、顕微鏡をのぞいたときの見た目も2倍になっている」ことになります。
 
 
次に、面積に関しては x² 倍となります。
これは面積を求めるときに〔長さ〕×〔長さ〕をするためですが、たとえば、一辺の長さが a, b の長方形の各辺を2倍ずつすると、2a, 2b となり、面積としては ab から 4ab に4倍されています。
つまり、面積としては、辺の長さの２乗倍（今回だと 2 の2乗）されたということです。

実際に顕微鏡をのぞいたときには交換前後で下の図のようなイメージとなり、三角形の面積は4倍になります。（対象物が視野の中で拡大される）

 
 
ただ、このとき、（プレパラートのうち）元々は左側の青丸全体部分を見ていたものが、中央の赤丸部分だけを拡大して見ていることになります。
つまり、「倍率を変えて拡大する」ことで「より狭い範囲を詳しく見ている」ことになり、視野の広さ（観察している部分）はそれだけ狭くなってしまっています。

左右の赤丸の面積比が 1：4（4倍に拡大）だとすると、倍率を変えても顕微鏡の筒の太さ等が変わるわけではないため左側の青の円も『4』の大きさということになります。つまり、倍率を変えたことで「元々の『4』のうちの『1』のエリアしか見ていない」ということになります。

ということで、「顕微鏡の倍率を（変える前と比べて） x 倍にすると、視野の広さは 1/x² 倍になる」ということになります。