| 〔質問〕 全体集合Uとその部分集合A、B、C、があり、 n(A)=20、n(B)=14、n(C)=18、 n(A∩B)=n(B∩C)=7、n(C∩A)=6 n(A∩B∩C)=3 である時、[A∩Bの補集合]∩[Cの補集合] の個数の求め方をお願いします |
| 〔回答〕 この手の問題が出てきた場合は、以下のような図を書いてもらって、各エリアの数を具体的に書き上げてしまってください! 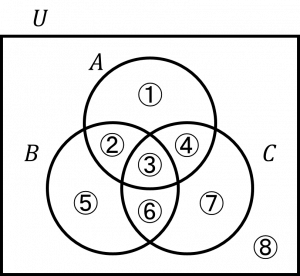 例えば、n(A)=20 というのは、①+②+③+④ が 20 ということですし、 n(A∩B)=7 というのは、②+③ が 7 というのを表していて、 n(A∩B∩C)=3 というのは、③ が 3 ということを表しています。 (つまり、② は 4) この要領で順番に計算していけば、すべてのエリアの数が求まると思います。 今回、求めるものは、[A∩Bの補集合](② と ③ でない所なので、①、④~⑧)と、[Cの補集合](①、②、⑤、⑧)の共通部分なので、その該当箇所を具体的に考えてしまってください! |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |


