| 〔質問〕 x2-(8-a)x+12-ab=0 が実数の定数aの値に関わらず実数解をもつとき、定数bの値の範囲を求めよ。 解いていく途中で出てくる2次方程式の a2+4(b-4)a+16=0 の判別式をDとすると、a2+4(b-4)a+16≧0 が全ての実数aに対して成り立つための条件が D≦0 となるのはなぜですか。教えてください。 |
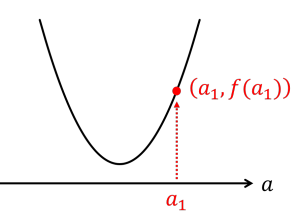
| 〔回答〕 「全ての実数aに対して a2+4(b-4)a+16≧0 が成り立つ」というのは、f(a)=a2+4(b-4)a+16 というのを考えてもらったときに、どんな a のときでも f(a) の値が 0以上」ということですので、下のグラフのように横軸に対して常に上側にある状態になっているはずです。 ※ ちょうど 0 になることがあってもいいので、横軸に接していてもかまいません。
ということは、 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |