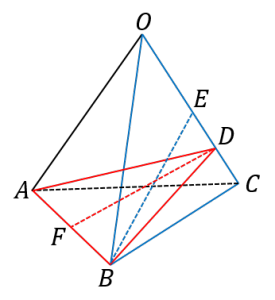
| 〔質問〕 「一辺が4cmの正四面体OABCがある。辺OC上にOD=3cmとなるように点Dをとるときの、△ABDの面積を求めなさい。」 という問題で、三平方の定理プラスルートが出てきてわけわかんなくなっちゃいます。よろしくお願いします。 |
| 〔回答〕 数学の問題全般に言えることですが、「問いに答えるためにはどうしたらよいか」を常に考えましょう!
【方針】 【実際の計算】 正四面体をつくる三角形はすべて正三角形です。 DE=OD-OE=3-2=1 △BEDは∠E=90°の直角三角形なので、三平方の定理が使えます。 また、△DFBは∠F=90°の直角三角形なので、三平方の定理が使えます。 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |