| 〔質問〕 A(1, 1) を通り、傾きがmの直線は定点公式より、y=m(x-1)+1 と表せますが、これだとこの直線がy軸に平行な直線、x=1 が表せません。なぜこのような齟齬が生じるのですか? |
| 〔回答〕 元々この公式は「傾きがある」ことを前提にして作られたもので、縦線自体が対象外になっているためです。 具体的には、例えば、点(a, b) を通り、傾きmの直線上の点を (x1, y1) とします。 直線の傾きは「y座標の変化分/x座標の変化分」で求まりますので、m=(y1-b)/(x1-a) が成り立ちます。(または m=(b-y1)/(a-x1)) 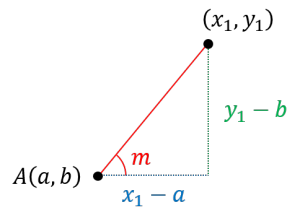 この式を整理してもらうと、m・(x1-a)=y1-b となり、y1=m・(x1-a)+b が出てくる、という仕組みです。 ところで、この計算では分母を x1-a としていますが、そもそも分数では分母は 0 であってはいけません。つまり、この段階で、x1≠a ということを前提としていたということになります。つまり、x方向に変化がなく、y方向だけ変化するような状況は対象外だった、ということです。ですので、この式では縦線を表すことができない、ということです。 なお、数Ⅱで習う ax+by+c=0 という形式であれば、縦線を含めたすべての直線を表現することができます。 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

