| 〔質問〕 2定点からの距離の2乗の差が一定の点の軌跡が、その2定点を結んだ直線と垂直に交わるのはなぜですか? |
| 〔回答〕 式で示すと、点P(a, b)、点Q(c, d)とし、求める直線上の点を R(x, y)とおくと、問題の条件から {(x-a)2+(y-b)2}-{(x-c)2+(y-d)2}=k(kは定数)とおけることになります。 この式を展開して整理すると(ふつうに展開するだけなので省略します)、x, y の1次式となるため「直線」ということがわかり、しかも傾きは-(a-c)/(b-d) となって、たしかに直線PQの傾きとは-1倍の関係になっています。 証明としてはこれを示せばOKです。 ですが、こうなる図形的な理由というか直感的なところの疑問だと思いますので、以下の図を見てください。 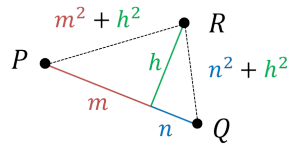 問題で言われていることは、「2定点からの距離の2乗」についてですので三平方の定理を考えればいいですが、まずは、点Rから直線PQに対して垂線を下ろしてみてください。このとき、PR2 は m2+h2、QR2 は n2+h2 ということになります。 で、この差が一定ということですが、よくよく考えてみると h の部分は共通ですので、結局 PR2-QR2 というのは m2-n2 のことだったということです。これは h の部分をもっと伸ばしたり縮めたりしても PR2-QR2 は m2-n2 のまま変わらないということです。 ※ 差となる定数kが与えられば、その値から垂線の足となる点が定まる。そこから h がどんな値をとったとしても PR2-QR2=m2-n2=k がキープされる。 本来説明としてはこれでは不十分ですが、結局以上のようなことを表しているんだと思ってもらったらいいと思います。 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

