| 〔質問〕 3つの方程式 ①、②、③ があり、 ・「① かつ ②」⇒「③」 ・「① かつ ③」⇒「②」 を満たすとき、「①かつ②」⇔「①かつ③」となる理由を教えてください |
| 〔回答〕 ・「かつ」というのは「共通部分」のこと ・「p ⇒ q」が真というのは「P が Q の一部(P が小、Q が大)」の関係 ということを踏まえて、以下のように考えてみてください。 (それぞれの解を集合として表しています) まず、「① かつ ②」⇒「③」が満たされているということは、① と ② の共通部分(図中 a と b)が、③ の一部になっていないといけないので、③ から漏れている a の部分は空集合(解が存在しない)ということになります。 一方、「① かつ ③」⇒「②」の方も、① と ③ の共通部分(図中 b と c)が、② の一部になっていないといけないので、② から漏れている c の部分は空集合になります。 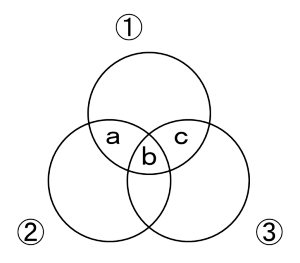 というわけで、「① かつ ②」も「① かつ ③」も、ともに「b」の部分を指すことになり、両者はちょうど一致します。 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

