| 〔質問〕 互いに外接している三つの円の中心をそれぞれA,B,Cとし、(半径は、中心がAの円<中心がBの円<中心がCの円)中心がAの円と中心がBの円の接点をD、中心がBの円と中心がCの円の接点をE、中心がCの円と中心がAの円の接点をFとします。 △ABCの内角の大きさが30°、60°、90°であるとき、△DEFの外接円は△ABCの内接円であるようなのですが、なぜそう言えるのかわかりません。 |
| 〔回答〕 私が問題の意味を間違っていなければ、このことはこの三角形でなくても成り立つと思います。(3つの円が接してさえいれば成り立つ) ちょっと逆からの説明になりますが、まず、三角形の内接円の中心(内心)というものを考えると、これは3つの角の二等分線の集まる箇所として求めることができます。点D, E, F は内心 I からそれぞれの辺に下した垂線の足とします。 このとき、以下の図のように、同じ色で塗っている2つの三角形はそれぞれ合同となります。 (△ADI≡△AFI, △BDI≡△BEI, △CEI≡△CFI) 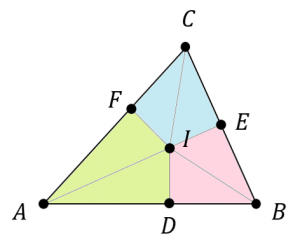 ということは、AD=AF、BD=BE、CE=CF となりますので、これをそれぞれ半径と見立てれば、円が書けることになります。 ※ ここでは半径は「中心がAの円<中心がBの円<中心がCの円」とはなっていませんが、適宜置き換えてください (逆に、「3つの三角形が互いに接している」から考えたとしても、必ずこのような形で三点 D, E, F が存在しています) 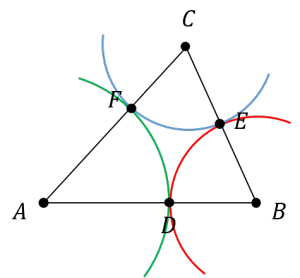 このとき、下図の円は、△ABCという意味では内接円になっていますが、各辺との接点である D, E, F はこの円上にありますので、△DEFから見れば外接円ということになっています。 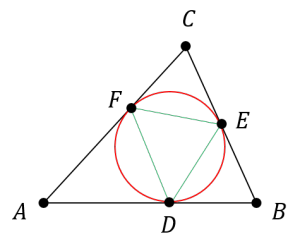 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

