| 〔質問〕 「背理法」による証明方法がいまいちピンときません。なぜこれでいいのですか? |
| 〔回答〕 消去法的に成り立つことになるからです。 |
背理法とは、命題 p ⇒ q というのが「偽」であると仮定して、その場合、矛盾が生じることを示すことで、「仮定したことがおかしい」 ので、命題 p ⇒ q は「真」だ、という証明方法です。
この論法がいまいち納得しにくい、という人は多いと思います。
そこで、以下のように考えてください。
※ まずは簡単に、ある要素がある集合のメンバーかどうか、について考えます。ちょうど「√2 は無理数である」のようなケースです。(集合のケースについてはこちら)
そもそも、要素 p と 集合 Q の関係性は以下の2パターンしかないわけです。
そのうち「p ⇒ q が真」というのは、① の場合に相当します。
(小文字の q は、集合 Q のメンバー、という意味。あえてアルファベットを変えています)
(図表1) そもそもこの2パターンのどちらかでしかない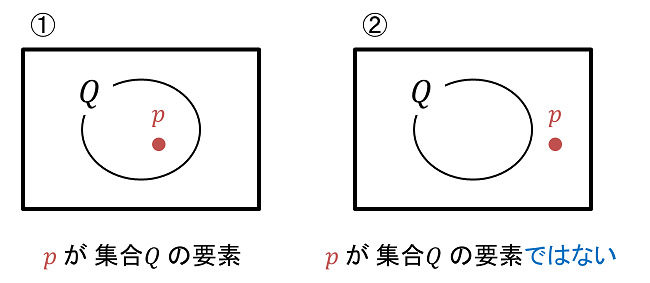 |
で、背理法における「命題の否定」というのは、この ① の否定(つまり ② の場合)についてどうなるかを見ているのです。
そして、② で何かしらおかしいことが生じれば、こうした状況は現実的には存在しえないということになります。
つまり、そもそも2パターンしかありえない状況で、そのうちの1つ(ここでは ② )がダメということで、消去法的に ① の「p は Q の一部」というケースしか残らないということになります。なので、元の命題 p ⇒ q は「真」ということになるのです。
(図表2) 消去法的に一方しか残らない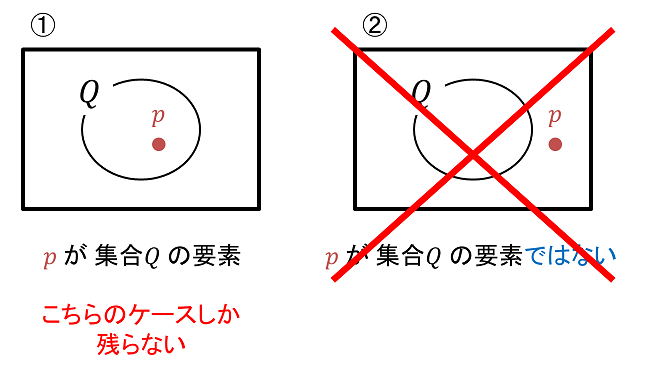 |
| アンケートへのご協力をお願いします(所要2~3分) |
|---|
| 「将来設計・進路」に関するアンケートを実施しています。ご協力いただける方はこちらよりお願いします (Googleフォームにアクセスします) |

